Viewing posts for the category Featured on frontpage
Visualizing the Earth's dipolar magnetic field
Posted by: christian in Featured on frontpage on 28 Aug 2019
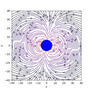
The magnetic field due to a magnetic dipole moment, $\boldsymbol{m}$ at a point $\boldsymbol{r}$ relative to it may be written $$ \boldsymbol{B}(\boldsymbol{r}) = \frac{\mu_0}{4\pi r^3}[3\boldsymbol{\hat{r}(\boldsymbol{\hat{r}} \cdot \boldsymbol{m}) - \boldsymbol{m}}], $$ where $\mu_0$ is the vacuum permeability. In geomagnetism, it is usual to write the radial and angular components of $\boldsymbol{B}$ as: $$ \begin{align*} B_r & = -2B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\cos\theta, \\ B_\theta & = -B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\sin\theta, \\ B_\phi &= 0, \end{align*} $$ where $\theta$ is polar (colatitude) angle (relative to the magnetic North pole), $\phi$ is the azimuthal angle (longitude), and $R_\mathrm{E}$ is the Earth's radius, about 6370 km. See below for a derivation of these formulae.
Impact craters on Earth
Posted by: christian in Featured on frontpage on 28 Jul 2019
The Earth Impact Database is a collection of images, publications and abstracts that provides information about confirmed impact structures for the scientific community. It is hosted at the Planetary and Space Science Centre (PASSC) of the University of New Brunswick.
Two-dimensional collisions
Posted by: christian in Featured on frontpage on 24 Jun 2019

This small Python project is a physical simulation of two-dimensional physics. The animation is carried out using Matplotlib's FuncAnimation method and is implemented by the class Simulation. Each "particle" of the simulation is represented by an instance of the Particle class and depicted as a circle with a fixed radius which undergoes elastic collisions with other particles.
Packing circles inside a shape
Posted by: christian in Featured on frontpage on 5 Jun 2019
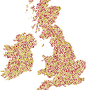
A previous blog post dealt with packing circles into a circle. To fill an arbitrary shape, a slightly different approach is needed. The code is presented in my github repo.
Simulating two-dimensional polycrystals
Posted by: christian in Featured on frontpage on 31 Mar 2019

The following code simulates (very approximately) the growth of a polycrystal from a number of seeds. Atoms are added to the crystal lattice of each of the resulting grains until no more will fit, creating realistic-looking boundaries where two grains meet.