Viewing posts for the category Featured on frontpage
The Kelvin wake pattern
Posted by: christian in Featured on frontpage on 20 Feb 2024
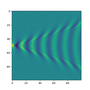
An object (ship, duck, etc.) travelling across the surface of water at a constant velocity $\boldsymbol{u}$ produces a characteristic wake pattern of waves first described by Lord Kelvin.
The two-dimensional wave equation
Posted by: christian in Featured on frontpage on 17 Feb 2024

The wave equation is a second-order linear partial differential equation describing the behaviour of mechanical waves; its two (spatial) dimensional form can be used to describe waves on a surface of water:
Analysing flight punctuality data for UK airports: I. Basic statistics for 2022
Posted by: christian in Featured on frontpage on 9 Feb 2024

The UK Civil Aviation Authority (CAA) publishes regular statistics on the punctuality of flights arriving at and departing UK airports. These data can be retrieved with the script available on the GitHub repository accompanying this blog article: get_data.py.
A circle problem
Posted by: christian in Featured on frontpage on 30 Sep 2023
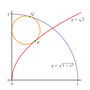
A recent tweet by @iwontoffendyou posed the following problem: with reference to the figure below, what is the radius of the orange circle, which is tangent to the $y$-axis, the unit circle and the curve $y = \sqrt{x}$?
The Weierstrass function
Posted by: christian in Featured on frontpage on 10 Nov 2022
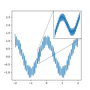
The Weierstrass function, named after the German mathematician Karl Weierstrass (1815 – 1897) is a real-valued function that is continuous everywhere but nowhere differentiable. It is usually expressed as a Fourier series: