Viewing posts for the category Featured on frontpage
Visualizing the Temperature in Cambridge, UK
Posted by: christian in Featured on frontpage on 31 Jul 2022
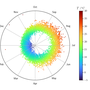
The Digital Technology Group (DTG) at Cambridge University has been recording the weather from the roof of their building since 1995. The complete data are available to download in CSV format from the DTG website as the file weather-raw.csv.
A "universal" formula for egg shape
Posted by: christian in Featured on frontpage on 19 Apr 2022
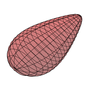
A recent article, Narushin et al., "Egg and math: introducing a universal formula for egg shape", Ann. N.Y. Acad. Sci. 1505, 169 (2021) introduces a "universal" formula for the shape of eggs, including "pyriform" (pear-shaped) eggs such as those of the guillemot – supposedly, such eggs roll in a circle when disturbed so that they do not fall off the cliffs where these birds nest.
Visualizing Kaczmarz's Algorithm
Posted by: christian in Featured on frontpage on 18 Mar 2022

Kaczmarz's algorithm is an iterative algorithm for solving a system of linear equations. In its simplest form, the equations are written in matrix form, $\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}$ and, starting with the initial guess for the solution, $\boldsymbol{x}_1 = \boldsymbol{0}$, the zero vector, successive approximations are generated by projecting $\boldsymbol{x}_k$ onto the hyperplanes defined by the rows of $\boldsymbol{A}$: $\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots$. $$ \boldsymbol{x}_{k+1} = \boldsymbol{x}_{k} + \frac{b_{i} - \boldsymbol{a}_i.\boldsymbol{x}_k}{|\boldsymbol{a}_i|^2} \boldsymbol{a}_i $$
Ridgeline plots of monthly UK temperatures
Posted by: christian in Featured on frontpage on 5 Feb 2022

The UK Meteorological Office offers historical data of mean monthly temperatures in different regions of the UK for download. For the purposes of this blog post, I downloaded the data corresponding to two regions: Scotland.txt and South_England.txt.
Linear least squares fitting of a two-dimensional data
Posted by: christian in Featured on frontpage on 30 Jan 2022

This earlier blog post presented a way of performing a non-linear least squares fit on two-dimensional data using a sum of (2D) Gaussian functions.