Viewing posts for the category Featured on frontpage
Direct linear least squares fitting of an ellipse
Posted by: christian in Featured on frontpage on 9 Aug 2021
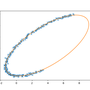
Fitting a set of data points in the $xy$ plane to an ellipse is a suprisingly common problem in image recognition and analysis. In principle, the problem is one that is open to a linear least squares solution, since the general equation of any conic section can be written $$ F(x, y) = ax^2 + bxy + cy^2 + dx + ey + f = 0, $$ which is linear in its parameters $a$, $b$, $c$, $d$, $e$ and $f$. The polynomial $F(x,y)$ is called the algebraic distance of any point $(x, y)$ from the conic (and is zero if $(x, y)$ happens to lie on the conic).
Chaotic Balls
Posted by: christian in Featured on frontpage on 27 Jul 2021

Inspired by this recent Numberphile video, here is a demonstration of chaos in a simple dynamical system: two balls, with near-identical starting conditions, bounce around elastically off a circular wall. After a short time, the balls' trajectories diverge completely.
Measurements of the electron charge over time
Posted by: christian in Featured on frontpage on 29 Mar 2021

In his 1986 book, Surely You're Joking, Mr. Feynman! physicist Richard Feynman writes:
Iceberg dynamics
Posted by: christian in Featured on frontpage on 22 Feb 2021

Prompted by this tweet and campaign for icebergs to be depicted in their most stable equilibrium orientation, here is a Python script modelling the dynamics of a two-dimensional iceberg which starts in an arbitrary orientation and position and relaxes under gravitational and buoyant forces to its most stable configuration. A cork floats "on its side": with its longest axis parallel to the water's surface (it doesn't bob around with its longest axis vertical), and an iceberg does the same.
Where are the world's nuclear power plants?
Posted by: christian in Featured on frontpage on 18 Feb 2021
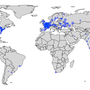
As of April 2020, there were 440 operational nuclear power reactors in the world. They are listed on this Wikipedia page, which can be scraped using the code at the bottom of this post for their important details, including their locations as latitude and longitude coordinates. The result of this scraping is the CSV file operational-nuclear-power-stations.csv, which can be analysed using pandas.