Viewing posts for the category Featured on frontpage
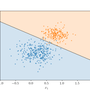
A shallow neural network for simple nonlinear classification
Posted by: christian in Featured on frontpage on 18 Sep 2020
Classification problems are a broad class of machine learning applications devoted to assigning input data to a predefined category based on its features. If the boundary between the categories has a linear relationship to the input data, a simple logistic regression algorithm may do a good job. For more complex groupings, such as in classifying the points in the diagram below, a neural network can often give good results.
Plotting the decision boundary of a logistic regression model
Posted by: christian in Featured on frontpage on 17 Sep 2020
In the notation of this previous post, a logistic regression binary classification model takes an input feature vector, $\boldsymbol{x}$, and returns a probability, $\hat{y}$, that $\boldsymbol{x}$ belongs to a particular class: $\hat{y} = P(y=1|\boldsymbol{x})$. The model is trained on a set of provided example feature vectors, $\boldsymbol{x}^{(i)}$, and their classifications, $y^{(i)} = 0$ or $1$, by finding the set of parameters that minimize the difference between $\hat{y}^{(i)}$ and $y^{(i)}$ in some sense.
Logistic regression for image classification
Posted by: christian in Featured on frontpage on 3 Sep 2020
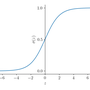
Simple logistic regression is a statistical method that can be used for binary classification problems. In the context of image processing, this could mean identifying whether a given image belongs to a particular class ($y=1$) or not ($y=0$), e.g. "cat" or "not cat". A logistic regression algorithm takes as its input a feature vector $\boldsymbol{x}$ and outputs a probability, $\hat{y} = P(y=1|\boldsymbol{x})$, that the feature vector represents an object belonging to the class. For images, the feature vector might be just the values of the red, green and blue (RGB) channels for each pixel in the image: a one-dimensional array of $n_x = n_\mathrm{height} \times n_\mathrm{width} \times 3$ real numbers formed by flattening the three-dimensional array of pixel RGB values. A logistic regression model is so named because it calculates $\hat{y} = \sigma(z)$ where $$ \sigma(z) = \frac{1}{1+\mathrm{e}^{-z}} $$ is the logistic function and $$ z = \boldsymbol{w}^T\boldsymbol{x} + b, $$ for a set of parameters, $\boldsymbol{w}$ and $b$. $\boldsymbol{w}$ is a $n_x$-dimensional vector (one component for each component of the feature vector) and b is a constant "bias".
The Maxwell–Boltzmann distribution in two dimensions
Posted by: christian in Featured on frontpage on 14 Jul 2020
This script demonstrates the relaxation of an ensemble of colliding particles towards the equilibrium, Maxwell-Boltzmann distribution of their speeds. Unlike this previous post, the collision detection and dynamics are handled using NumPy arrays without explicit python loops (except over collision pairs), which improves the performance greatly.
Visualizing the real forms of the spherical harmonics
Posted by: christian in Featured on frontpage on 15 Jun 2020
The spherical harmonics are a set of special functions defined on the surface of a sphere that originate in the solution to Laplace's equation, $\nabla^2f=0$. Because they are basis functions for irreducible representations of SO(3), the group of rotations in three dimensions, they appear in many scientific domains, in particular as the angular part of the wavefunctions of atoms (atomic orbitals). They are described in terms of an integer degree $l=0,1,2,\ldots$ and order $m=-l,-l+1,\ldots,l$.