The Kelvin wake pattern

Posted by: christian on 20 Feb 2024

An object (ship, duck, etc.) travelling across the surface of water at a constant velocity $\boldsymbol{u}$ produces a characteristic wake pattern of waves first described by Lord Kelvin.

A duck and its wake

In his model of the effect, he assumed deep, still water, neglected surface tension, and restricted the magnitude of the pressure causing the wave to be small enough that the relevant equations of motion could be treated as linear. With these assumptions, the wave vector associated with a periodic disturbance, $\boldsymbol{k} = k_x\boldsymbol{\hat{x}} + k_y\boldsymbol{\hat{y}}$ oscillates at an angular frequency of $\omega(\boldsymbol{k}) = \sqrt{g|\boldsymbol{k}|}$, where $g$ is the gravitational acceleration and the magnitude of the wave vector is related to the wavelength through $\lambda = 2\pi / |\boldsymbol{k}|$.

The change due to the waves in the water height is then

$$ z(\boldsymbol{r},t) = \int A(\boldsymbol{k}) \exp[i(\boldsymbol{k}.\boldsymbol{r} - \omega t)]\,\mathrm{d}^2\boldsymbol{k}, $$

where $A(\boldsymbol{k})$ is the amplitude of the wave with wave vector $\boldsymbol{k}$.

In the reference frame of a ship (duck, etc.) causing such a disturbance the water appears to be moving at velocity $-\boldsymbol{u}$ and $\omega(\boldsymbol{k}) = \sqrt{g|\boldsymbol{k}|} - \boldsymbol{u}.\boldsymbol{k}$. In this frame the wake appears as the interference pattern of stationary waves: $\omega(\boldsymbol{k}) = 0$ and therefore:

$$ g|\boldsymbol{k}| = (\boldsymbol{u}.\boldsymbol{k})^2 = |\boldsymbol{k}|^2 (\boldsymbol{u}.\boldsymbol{\hat{k}})^2 \;\Rightarrow\; |\boldsymbol{k}| = \frac{g}{(\boldsymbol{u}.\boldsymbol{\hat{k}})^2}. $$

That is,

$$ \boldsymbol{k} = |\boldsymbol{k}|\boldsymbol{\hat{k}} = \frac{g}{(\boldsymbol{u}.\boldsymbol{\hat{k}})^2}\boldsymbol{\hat{k}}, $$

where the unit vector, $\boldsymbol{\hat{k}} = (\cos\theta, \sin\theta)$ with $\theta$ measured with respect to the direction of $\boldsymbol{u}$: that is, $\boldsymbol{u}.\boldsymbol{\hat{k}} = u\cos\theta$.

Therefore,

$$ z(\boldsymbol{r}) = \int_0^{2\pi} A(\theta) \exp \left[ ig\frac{\boldsymbol{r}.\boldsymbol{\hat{k}}}{(\boldsymbol{u}.\boldsymbol{\hat{k}})^2} \right]\,\mathrm{d}\theta. $$

Now, assume that $A$ is constant for $-\frac{\pi}{2} < \theta < \frac{\pi}{2}$ and zero elsewhere: the ship disturbs the water equally in the immediate vicinity of its stern. Writing $\boldsymbol{r}$ in polar coordinates: $\boldsymbol{r} = r(\cos\phi, \sin\phi)$, we have

$$ \boldsymbol{r}.\boldsymbol{\hat{k}} = r(\cos\theta\cos\phi + \sin\theta\sin\phi) = r\cos(\theta - \phi) $$

and

$$ z(\phi, r) = \int_{-\pi/2}^{\pi/2} \exp\left[ ig\frac{r\cos(\theta-\phi)}{u^2\cos^2\theta} \right]\,\mathrm{d}\theta = \int_{-\pi/2}^{\pi/2} \cos\left[ \rho \frac{\cos(\theta-\phi)}{\cos^2\theta} \right]\,\mathrm{d}\theta, $$

where $\rho = rg/u^2$. There are further approximations that can yield a solution for $z(\phi, r)$ in terms of Airy functions but the code below evaluates the integral numerically and produces the following plot.

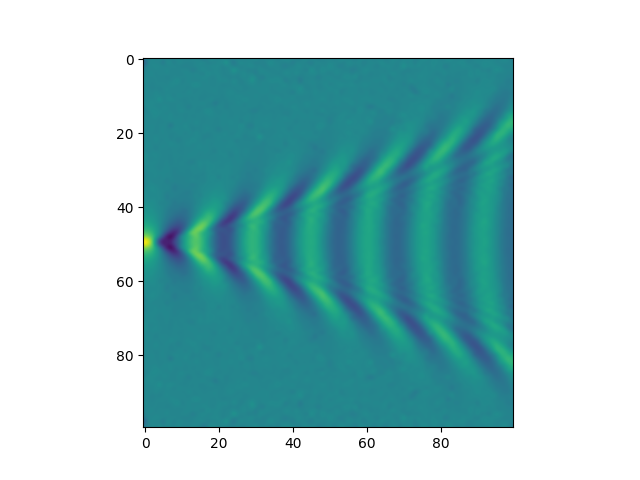
enter image description here

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad

# Our ship (boat, duck) is travelling to the left but we're in its
# reference frame so it looks stationary at (0, 0).
nx, ny = 100, 100
xgrid, ygrid = np.linspace(0, 40, nx), np.linspace(-20, 20, ny)
X, Y = np.meshgrid(xgrid, ygrid)
# The wake wave height will be calculated at each point of this array.
z = np.empty((ny, nx))

def func(theta, rho, phi):
    return np.cos(rho * np.cos(theta-phi) / np.cos(theta)**2)

for j, x in enumerate(xgrid):
    for i, y in enumerate(ygrid):
        rho = np.linalg.norm((x, y))
        phi = np.arctan2(y, x)
        z[i, j] = quad(func, -np.pi/2, np.pi/2, args=(rho, phi))[0]

plt.imshow(z, interpolation="bicubic")
plt.savefig("kelvin-wake.png")

Comments

Comments are pre-moderated. Please be patient and your comment will appear soon.

Elie RAPHAEL 2 months ago

Thanks Christian for the great blog post on the Kelvin wake pattern! In some cases the angle between the two branches of the V seems to be smaller than predicted by Kelvin. Frédéric Dias published a nice review paper on this 10 years ago. See: Journal of Fluid Mechanics , Volume 746 , May 10, 2014 (https://doi.org/10.1017/jfm.2014.69)

Link | Reply

christian 2 months ago

Interesting! I didn't know about this paper – thank you.
Cheers, Christian