Posted by: christian on 31 Mar 2019
The following code simulates (very approximately) the growth of a polycrystal from a number of seeds. Atoms are added to the crystal lattice of each of the resulting grains until no more will fit, creating realistic-looking boundaries where two grains meet.
Two sorts of lattice are supported, 'hex' and 'square'. On each iteration of the main loop in Crystal.grow_crystal() an existing atom is selected at random and its neighbouring lattice sites are examined to see if a new atom will fit there. If no such sites are available, the atom becomes 'inactive' and won't be selected in future.
To avoid having to compute the distance to each of the already-placed atoms in the simulation to see if a new atom will fit on a site, the crystal's domain is divided into square cells of length equal to two atom diameters and every atom is assigned to a cell; it is only necessary to examine atoms placed in the same cell as a candidate site and its immediate neighbouring cells – we know that atoms in cells further away cannot be too close to the candidate site.
Some example usage cases are given below: extra features include (a) colouring the atoms in each grain; (b) customizing the style in which an atom is drawn; (c) representing the atoms as circles or space-filling polygons appropriate to the lattice type.
Example 1
crystal = Crystal(ngrains=5, seed_minimum_distance=0.3, lattice='square',
d=0.03)
crystal.grow_crystal()
crystal.save_atom_positions()
colours = plt.get_cmap("tab10").colors
crystal.plot_crystal(colours=colours)
Example 2
crystal = Crystal(ngrains=15, seed_minimum_distance=0.1, lattice='hex',
d=0.03)
crystal.grow_crystal()
crystal.save_atom_positions()
colours = plt.get_cmap("tab10").colors
crystal.plot_crystal(colours=colours, circular_atoms=False)
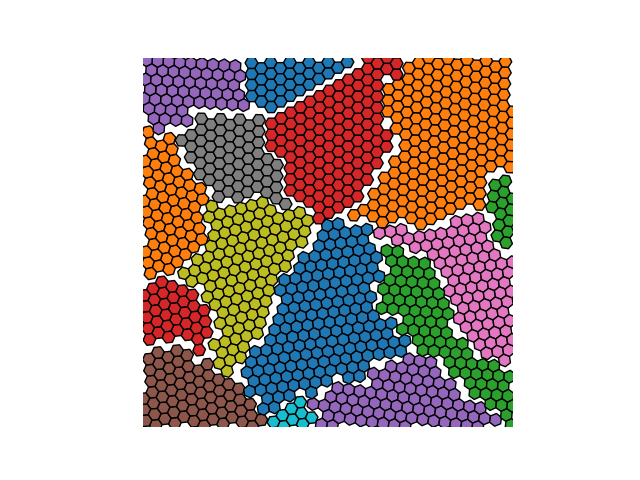
Example 3
crystal = Crystal(ngrains=32, seed_minimum_distance=0.05, lattice='hex',
d=0.01)
crystal.grow_crystal()
crystal.save_atom_positions()
crystal.plot_crystal(linewidth=0)
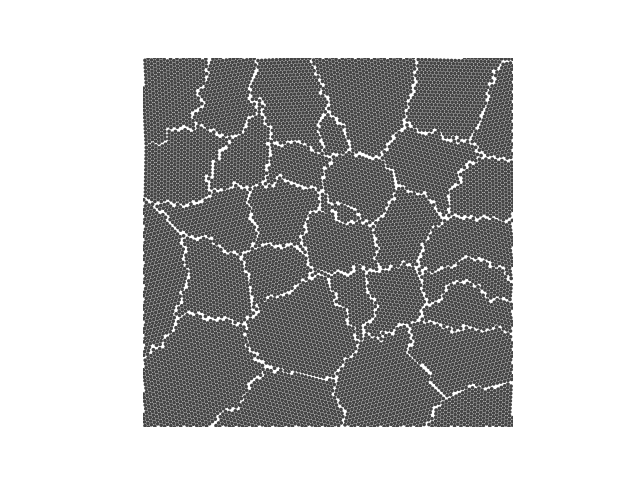
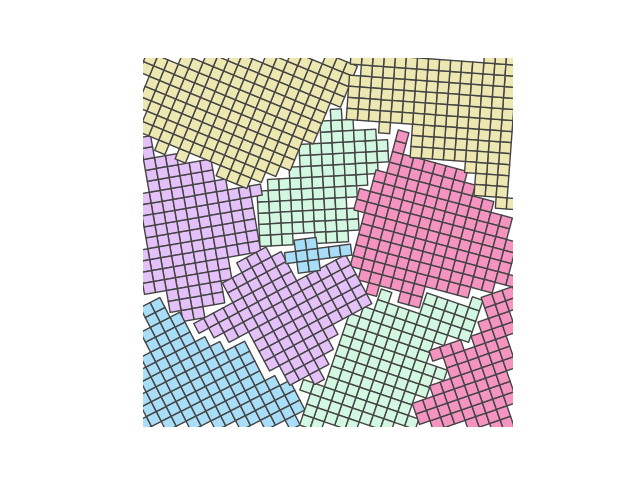
Example 4
crystal = Crystal(ngrains=10, seed_minimum_distance=0.1, lattice='square',
d=0.03)
crystal.grow_crystal()
crystal.save_atom_positions()
colours = ['#d3f8e2', '#e4c1f9', '#f694c1', '#ede7b1', '#a9def9']
crystal.plot_crystal(colours=colours, edgecolor='#444444', circular_atoms=False)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import PatchCollection
import random
class Atom:
"""A simple atom in a 2-D crystal grain, with its coordinates."""
def __init__(self, grain, coords):
self.grain = grain
self.coords = coords
class Grain:
"""A grain in a 2-D (poly-)crystal.
grain_id is the unique ID of the grain, seed is the (x,y) coordinates of
the first atom placed in the grain, and lattice is a string identifying
which kind of crystal lattice to use ('hex' or 'square').
"""
def __init__(self, grain_id, seed, lattice='hex'):
self.grain_id = grain_id
self.seed = seed
self.lattice = lattice
# Initialize the displacements for other atoms around a reference atom,
# and the maximum rotation angle, phi, to obtain all orientations.
if lattice == 'hex':
# Hexagonal lattice: 6 other atoms in a hexagonal pattern.
a, b = 0.5, np.sqrt(3)/2
self.lattice_disp = np.array(
[[a,-b],[1,0],[a,b],[-a,b],[-1,0],[-a,-b]]).T
self.phi = np.pi / 3
elif lattice == 'square':
# Square lattice: 4 other atoms placed orthogonally.
self.lattice_disp = np.array([[1.,0],[0,1.],[-1.,0],[0,-1.]]).T
self.phi = np.pi / 2
else:
sys.exit('Undefined lattice type: {}'.format(lattice))
# Rotate the displacements by some random angle up to phi.
self.setup_rotated_displacements()
def setup_rotated_displacements(self):
"""Rotate atom displacements at random to change the orientation."""
def _make_rot_matrix(alpha):
return np.array([[np.cos(alpha), -np.sin(alpha)],
[np.sin(alpha), np.cos(alpha)]])
theta = np.random.rand() * self.phi
# Two-dimensional rotation matrix.
self.rot = _make_rot_matrix(theta)
self.lattice_disp = (self.rot @ self.lattice_disp).T
patch_rot = _make_rot_matrix(self.phi/2)
if self.lattice == 'hex':
a = 1 / np.sqrt(3)
else:
a = 1 / np.sqrt(2)
self.patch_disp = a * (patch_rot @ self.lattice_disp.T).T
def distance(p, q):
"""Return the Euclidean distance between points p and q."""
return np.hypot(*(p-q))
class SimCells:
"""A region of the simulation area to search for neighbours.
To save us from calculating all the pairwise distances, keep track of
the location of atoms in "cells": for a given candidate site, we then only
need to look within that site's cell and its immediate neighbouring cells.
"""
def __init__(self, d):
"""Initialize the cell size and the array of cells."""
self.n = int(1 / 2 / d)
self.a = 1 / self.n
self.cell_array = [[[] for i in range(self.n)] for j in range(self.n)]
def _get_cell_indexes_from_atom_coords(self, coords):
"""Return the indexes ix, iy of the cell containing point coords."""
x, y = coords
return int(x / self.a), int(y / self.a)
def _get_atom_cell(self, atom):
"""Return the cell containing atom."""
ix, iy = self._get_cell_indexes_from_atom_coords(atom.coords)
return self.cell_array[ix][iy]
def add_atom_to_cell(self, atom):
"""Add atom to the appropriate cell."""
self._get_atom_cell(atom).append(atom)
def neighbouring_atoms_generator(self, coords):
"""Return a generator yielding all atoms "near" point coords."""
ix, iy = self._get_cell_indexes_from_atom_coords(coords)
dxy = ((0,0), (1,0), (1,1), (0,1),
(-1,1), (-1,0), (-1,-1), (0,-1), (-1,1))
for dx, dy in dxy:
ixx, iyy = ix+dx, iy+dy
if not (0 <= ixx < self.n and 0 <= iyy < self.n):
continue
for atom in self.cell_array[ixx][iyy]:
yield atom
class Crystal:
"""A simulation of a two-dimensional polycrystal."""
def __init__(self, ngrains=5, seed_minimum_distance=0.2, lattice='hex',
d=0.02):
"""Initialise the polycrystal.
ngrains is the number of grains, to be placed randomly on the unit
square with a minumum distance, seed_minimum_distance, between them.
hex = 'hex' or 'square' is the crystalline lattice type and d is the
atom diameter.
"""
self.ngrains = ngrains
self.seed_minimum_distance = seed_minimum_distance
self.lattice = lattice
self.d = d
self.atoms, self.grains = [], []
def seed_grains(self):
"""Place the ngrain seeds randomly, a minimum distane apart."""
# Reset the crystal.
self.atoms, self.grains = [], []
self.sim_cells = SimCells(self.d)
for i in range(self.ngrains):
while True:
site = np.random.random((2,))
for atom in self.atoms:
if distance(site,atom.coords) < self.seed_minimum_distance:
# Seed atom too close to another: go back and try again
break
else:
# Initialise a grain and add its seed atom.
grain = Grain(i, site, self.lattice)
self.grains.append(grain)
atom = Atom(grain, site)
self.atoms.append(atom)
self.sim_cells.add_atom_to_cell(atom)
break
def grow_crystal(self):
"""Grow a new polycrystal."""
self.seed_grains()
# i_active is a list of the indices of atoms whcih have space next
# to them to place a new atom.
i_active = list(range(self.ngrains))
while i_active:
# Pick a random "active" atom, and get its neighbouring lattice
# sites with enough space to place a new atom
i = np.random.choice(i_active)
candidate_sites = self.get_neighbour_candidate_sites(self.atoms[i])
if not candidate_sites:
# No candidate site was found: the atom is no longer active.
i_active.remove(i)
continue
# Add the atom and mark it as active (until we know better).
n = len(self.atoms)
atom = Atom(self.atoms[i].grain, random.choice(candidate_sites))
self.atoms.append(atom)
self.sim_cells.add_atom_to_cell(atom)
i_active.append(n)
print(len(self.atoms), 'atoms placed')
def get_neighbour_candidate_sites(self, atom):
"""Return candidate locations next to atom to place a new atom.
Look for sites on the crystal lattice of the grain of the provided
atom with enough space to locate a new atom and return a list of
the site coordinates.
"""
neighbour_sites = atom.coords + self.d * atom.grain.lattice_disp
candidate_sites = []
for site in neighbour_sites:
if not (0 <= site[0] < 1 and 0 <= site[1] < 1):
continue
# neighbouring_atoms_generator spits out atoms in the
# vicinity of site, using our array of "SimCells".
neighbouring_atoms_generator = self.sim_cells.\
neighbouring_atoms_generator(site)
for other_atom in neighbouring_atoms_generator:
if distance(site, other_atom.coords) < self.d * 0.99:
break
else:
candidate_sites.append(site)
return candidate_sites
def save_atom_positions(self, filename='crystal.out'):
"""Save the atom diameter and all atom locations to filename."""
with open(filename, 'w') as fo:
print('d =', self.d, file=fo)
for atom in self.atoms:
print(atom.coords[0], atom.coords[1], file=fo)
def _get_patch_vertices(self, atom):
return atom.coords + self.d * atom.grain.patch_disp
def plot_crystal(self, filename='crystal.png', circular_atoms=True,
colours=None, **kwargs):
"""Create a Matplotlib image of the polycrystal as filename.
If colours is None, use a single colour for all atoms; otherwise
a sequence of colours to cycle through for each grain can be
provided. Additional kwargs are passed straight to the PatchCollection
call that controls the drawing style of the atoms.
If circular_atoms is not True, each atom is represented by the shape of
its lattice (square or hexagon).
"""
if not colours:
# Atoms are boring grey if no alternative is provided.
colours = ['#444444']
ncolours = len(colours)
if not kwargs:
kwargs = {'linewidth': 1, 'edgecolor': 'k'}
fig, ax = plt.subplots()
# We have a bit of book-keeping to do: group the atoms into their
# grains in this dictionary, keyed by the grain_id.
grains = {}
for atom in self.atoms:
grains.setdefault(atom.grain.grain_id, []).append(atom)
for j,atoms in grains.items():
if circular_atoms:
patches = [plt.Circle(atom.coords, radius=self.d/2)
for atom in atoms]
else:
patches = [plt.Polygon(self._get_patch_vertices(atom))
for atom in atoms]
c = PatchCollection(patches, facecolor=colours[j % ncolours],
**kwargs)
ax.add_collection(c)
# Ensure the Axes are square and remove the spines, ticks, etc.
ax.set_aspect('equal', 'box')
plt.axis('off')
plt.savefig(filename)
plt.show()
crystal = Crystal(ngrains=10, seed_minimum_distance=0.2, lattice='square',
d=0.02)
crystal.grow_crystal()
crystal.save_atom_positions()
colours = plt.get_cmap("tab10").colors
crystal.plot_crystal(colours=colours)
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
Sarah 2 years ago
This is such a nice way to simulate those results wih cristals. Since I'm new to the python language, it was very enlightening how you wrote the code, not too much stuff to make it too hard. Will be trying this out. Thanks.
Link | ReplyAnandaram Mandyam 2 years ago
Nice and have rated it at 5 !
Link | ReplyNew Comment