Viewing posts by christian
An Arepo (Latin Wordle) Solver
Posted by: christian on 10 Jan 2022
Arepo is a word-guessing game like Wordle, but in Latin. Therefore, the Wordle-solving script presented previously can be used to solve Arepo problems, but a list of five-letter Latin words is required.
A Python Wordle Solver
Posted by: christian on 7 Jan 2022

Wordle is a daily online word-guessing game. The goal is to deduce the hidden five-letter word in as few guesses as possible: after each guess, the player is told which letters which match in the correct position (highlighted in green), which letters are present in the hidden word, but in a different position (highlighted in yellow) and which letters are not present (after those highlighted in green or yellow; these letters are presented on a grey background).
COVID deaths and vaccination rates
Posted by: christian in Featured on frontpage on 3 Jan 2022

The Python script below generates the following visualization of COVID deaths per 100,000 people for two classes of European country: those with less than 75% of the population vaccinated and those with at least this percentage vaccinated. The ongoing (as of January 2022) third wave of infections is causing fewer deaths in the countries with a higher vaccination rate.
The Klein–Nishina formula
Posted by: christian in Featured on frontpage on 18 Dec 2021

The Klein–Nishina formula gives the differential cross section for the scattering of photons off an electron. At low energies, light scatters elastically (Thomson scattering); at higher energies (for example, gamma radiation), inelastic Compton scattering occurs. In terms of the incoming and outgoing photon wavelengths, $\lambda$ and $\lambda'$:
Manufacturing Cobalt-60
Posted by: christian on 20 Nov 2021
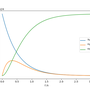
Lecture 12 of the MIT course 22.01: Introduction to Nuclear Engineering and Ionizing Radiation covers the manufacture of $\mathrm{^{60}Co}$ by neutron irradiation of $\mathrm{^{59}Co}$ in a research reactor. The thermal neutron absorption cross section of $\mathrm{^{59}Co}$ is $\sigma_0 \approx 20 \; \mathrm{barn}$, so for a neutron flux $\Phi$, the rate of change of the number of $\mathrm{^{59}Co}$ nuclei, $N_0$, may be written $$ \frac{\mathrm{d}N_0}{\mathrm{d}t} = -\sigma_0 \Phi N_0 \quad\Rightarrow N_0(t) = N_0(0)\mathrm{e}^{-\sigma_0\Phi t} $$