Viewing posts by christian
The Weierstrass function
Posted by: christian in Featured on frontpage on 10 Nov 2022
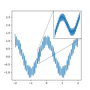
The Weierstrass function, named after the German mathematician Karl Weierstrass (1815 – 1897) is a real-valued function that is continuous everywhere but nowhere differentiable. It is usually expressed as a Fourier series:
Visualizing the Temperature in Cambridge, UK
Posted by: christian in Featured on frontpage on 31 Jul 2022
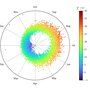
The Digital Technology Group (DTG) at Cambridge University has been recording the weather from the roof of their building since 1995. The complete data are available to download in CSV format from the DTG website as the file weather-raw.csv.
A "universal" formula for egg shape
Posted by: christian in Featured on frontpage on 19 Apr 2022
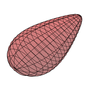
A recent article, Narushin et al., "Egg and math: introducing a universal formula for egg shape", Ann. N.Y. Acad. Sci. 1505, 169 (2021) introduces a "universal" formula for the shape of eggs, including "pyriform" (pear-shaped) eggs such as those of the guillemot – supposedly, such eggs roll in a circle when disturbed so that they do not fall off the cliffs where these birds nest.
Visualizing Kaczmarz's Algorithm
Posted by: christian in Featured on frontpage on 18 Mar 2022
Kaczmarz's algorithm is an iterative algorithm for solving a system of linear equations. In its simplest form, the equations are written in matrix form, $\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}$ and, starting with the initial guess for the solution, $\boldsymbol{x}_1 = \boldsymbol{0}$, the zero vector, successive approximations are generated by projecting $\boldsymbol{x}_k$ onto the hyperplanes defined by the rows of $\boldsymbol{A}$: $\boldsymbol{a}_1, \boldsymbol{a}_2, \ldots$. $$ \boldsymbol{x}_{k+1} = \boldsymbol{x}_{k} + \frac{b_{i} - \boldsymbol{a}_i.\boldsymbol{x}_k}{|\boldsymbol{a}_i|^2} \boldsymbol{a}_i $$
ASCII art
Posted by: christian on 17 Mar 2022
This is just a simple script that takes an image and renders it as a grid of ASCII characters in the console. The character chosen depends on the brightness of each pixel in the image: the following sequence (from densest (brightest) to least dense) is used: