Viewing posts by christian
Where are the world's nuclear power plants?
Posted by: christian in Featured on frontpage on 18 Feb 2021
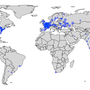
As of April 2020, there were 440 operational nuclear power reactors in the world. They are listed on this Wikipedia page, which can be scraped using the code at the bottom of this post for their important details, including their locations as latitude and longitude coordinates. The result of this scraping is the CSV file operational-nuclear-power-stations.csv, which can be analysed using pandas.
Making a word search puzzle in Python
Posted by: christian on 8 Feb 2021
The program given below takes a list of words and attempts to fit them into a grid with given dimensions to make a word search puzzle.
For example, using the file planets.txt:
Cistercian Numerals
Posted by: christian in Featured on frontpage on 5 Feb 2021
The Cistercian numeral counting system used by the Cistercian monastic order in the late medieval period. The digits 1 – 9 are depicted as symbols arranged around a vertical stave. By placing these symbols reflected vertically and/or horizontally into each of four locations the decimal digits in the units, tens, hundreds and thousands positions could be represented, enabling the numbers 0 – 9999 to be defined, as shown below (by user Meteoorkip from Wikipedia, CC BY-SA 4.0):
Old-style Matplotlib charts
Posted by: christian in Featured on frontpage on 22 Jan 2021
Just a quick demonstration of using Matplotlib and Pillow to customize a chart in the style of a 1950s academic journal article.
Rating the Novels of Agatha Christie
Posted by: christian on 22 Jan 2021
