Cistercian Numerals
Posted on 05 February 2021
The Cistercian numeral counting system used by the Cistercian monastic order in the late medieval period. The digits 1 – 9 are depicted as symbols arranged around a vertical stave. By placing these symbols reflected vertically and/or horizontally into each of four locations the decimal digits in the units, tens, hundreds and thousands positions could be represented, enabling the numbers 0 – 9999 to be defined, as shown below (by user Meteoorkip from Wikipedia, CC BY-SA 4.0):
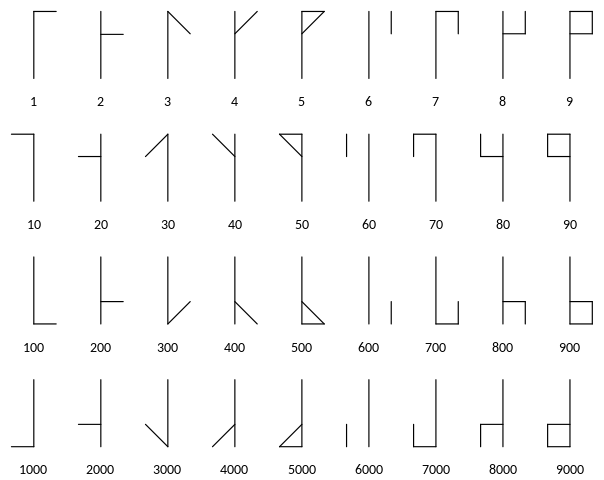
For example, the number 8759 is represented by:

The Python code below produces an SVG image with all 10000 Cistercian numerals depicted. The only really interesting part of it is the generation of the digits, which are represented as SVG path elements, defined in the directory d_paths, keyed by (i, d), where d is the digit for the ith decimal position (0=units, ..., 3=thousands). The paths for units position are defined explicitly; those for the other positions are obtained by the appropriate reflections.

# The paths to create the digits 1–9 in the "units" position.
d_paths = {
(0, 1): ((1, 0), (2, 0)),
(0, 2): ((1, 1), (2, 1)),
(0, 3): ((1, 0), (2, 1)),
(0, 4): ((1, 1), (2, 0)),
(0, 5): ((1, 1), (2, 0), (1, 0)),
(0, 6): ((2, 0), (2, 1)),
(0, 7): ((1, 0), (2, 0), (2, 1)),
(0, 8): ((1, 1), (2, 1), (2, 0)),
(0, 9): ((1, 1), (2, 1), (2, 0), (1, 0)),
}
# Generate the paths for the digits in the 10s, 100s and 1000s position by
# reflection.
for i in range(1, 10):
d_paths[(1, i)] = [(2-x, y) for x, y in d_paths[(0, i)]]
d_paths[(2, i)] = [(x, 3-y) for x, y in d_paths[(0, i)]]
d_paths[(3, i)] = [(2-x, 3-y) for x, y in d_paths[(0, i)]]
def transform(x, y, dx, dy, sc):
"""Transform the coordinates (x, y) into the scaled, displaced system."""
return x*sc + dx, y*sc + dy
def get_path(i, d):
"""Return the SVG path to render the digit d in decimal position i."""
if d == 0:
return
path = d_paths[(i, d)]
return 'M{},{} '.format(*transform(*path[0], *tprms)) + ' '.join(
['L{},{}'.format(*transform(*xy, *tprms)) for xy in path[1:]])
def make_digit(i, d):
"""Output the SVG path element for digit d in decimal position i."""
print('<path d="{}"/>'.format(get_path(i, d)), file=fo)
def make_stave():
"""Output the SVG line element for the vertical stave."""
x1, y1 = transform(1, 0, *tprms)
x2, y2 = transform(1, 3, *tprms)
print('<line x1="{}" y1="{}" x2="{}" y2="{}"/>'.format(x1, y1, x2, y2),
file=fo)
def svg_preamble(fo):
"""Write the SVG preamble, including the styles."""
# Set the path stroke-width appropriate to the scale.
stroke_width = max(1.5, tprms[2] / 5)
print("""<?xml version="1.0" encoding="utf-8"?>
<svg xmlns="http://www.w3.org/2000/svg"
xmlns:xlink="http://www.w3.org/1999/xlink" width="2000" height="2005" >
<defs>
<style type="text/css"><![CDATA[
line, path {
stroke: black;
stroke-width: %d;
stroke-linecap: square;
}
path {
fill: none;
}
]]>
</style>
</defs>
""" % stroke_width, file=fo)
def make_numeral(n, fo):
"""Output the SVG for the number n using the current transform."""
make_stave()
for i, s_d in enumerate(str(n)[::-1]):
make_digit(i, int(s_d))
# Transform parameters: dx, dy, scale.
tprms = [5, 5, 5]
with open('all_cistercian_numerals.svg', 'w') as fo:
svg_preamble(fo)
for i in range(10000):
# Locate this number at the position dx, dy = tprms[:2].
tprms[0] = 15 * (i % 125) + 5
tprms[1] = 25 * (i // 125) + 5
make_numeral(i, fo)
print("""</svg>""", file=fo)