Viewing posts by christian
Deleting Gmail messages by label with the Google API
Posted by: christian on 28 Jul 2023
Google's suite of APIs and their Python bindings can be used to delete emails automatically, saving the hassle of navigating page after page of 100 emails at a time. Setting up a Developer project, configuring OAuth access etc. is described on the Google Developers page here. Don't forget to add yourself as a Test User.
Modular arithmetic on a circle
Posted by: christian on 27 Jul 2023

Inspired by David Richeson's applet on GeoGebra the Python script below plots the lines joining pairs of points, evenly spaced on the perimeter of a circle according to the following algorithm: label the $n$ points $k=0, 1, 2, \ldots n-1$; then join point $k$ to point $mk\,\mathrm{mod}\,n$.
The Goat Problem
Posted by: christian on 29 Dec 2022
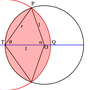
A goat is tethered on the perimeter of a circular paddock of grass by a rope of length $r$. What should $r$ be to allow the goat to graze on a maximum of half the area of the paddock?
Maurer Roses
Posted by: christian on 29 Nov 2022

A Maurer rose is a shape formed by connecting the points on a rose defined in the polar coordinate system by $r = \sin(n\theta)$ for some positive integer, $n$. The points to join are, in polar coordinates using degrees:
New York Times Spelling Bee solver
Posted by: christian on 29 Nov 2022
The New York Times publishes a daily puzzle, Spelling Bee, in which players must find as many words as possible using seven letters arranged in a hexagon. Each letter may be used any number of times but the solution words must be at least four letters long and must include the letter at the centre of the hexagon.