A blog of Python-related topics and code.
The Morse oscillator
Posted by: christian on 11 May 2019
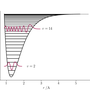
The Morse oscillator is a model for a vibrating diatomic molecule that improves on the simple harmonic oscillator model in that the vibrational levels converge with increasing energy and that at some finite energy the molecule dissociates. The potential energy varies with displacement of the internuclear separation from equilibrium, $x = r - r_\mathrm{e}$ as: $$ V(x) = D_\mathrm{e}\left[ 1-e^{-ax} \right]^2, $$ where $D_\mathrm{e}$ is the dissociation energy, $a = \sqrt{k_\mathrm{e}/2D_\mathrm{e}}$, and $k_\mathrm{e} = (\mathrm{d}^2V/\mathrm{d}x^2)_\mathrm{e}$ is the bond force constant at the bottom of the potential well.
The harmonic oscillator wavefunctions
Posted by: christian on 11 May 2019
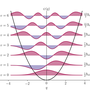
The harmonic oscillator is often used as an approximate model for the behaviour of some quantum systems, for example the vibrations of a diatomic molecule. The Schrödinger equation for a particle of mass $m$ moving in one dimension in a potential $V(x) = \frac{1}{2}kx^2$ is $$ -\frac{\hbar^2}{2m}\frac{\mathrm{d}^2\psi}{\mathrm{d}x^2} + \frac{1}{2}kx^2\psi = E\psi. $$ With the change of variable, $q = (mk/\hbar^2)^{1/4}x$, this equation becomes $$ -\frac{1}{2}\frac{\mathrm{d}^2\psi}{\mathrm{d}q^2} + \frac{1}{2}q^2\psi = \frac{E}{\hbar\omega}\psi, $$ where $\omega = \sqrt{k/m}$. This differential equation has an exact solution in terms of a quantum number $v=0,1,2,\cdots$: $$ \psi(q) = N_vH_v(q)\exp(-q^2/2), $$ where $N_v = (\sqrt{\pi}2^vv! )^{-1/2}$ is a normalization constant and $H_v(q)$ is the Hermite polynomial of order $v$, defined by: $$ H_v(q) = (-1)^ve^{q^2}\frac{\mathrm{d}^v}{\mathrm{d}q^v}\left(e^{-q^2}\right). $$ The Hermite polynomials obey a useful recursion formula: $$ H_{n+1}(q) = 2qH_n(q) - 2nH_{n-1}(q), $$ so given the first two: $H_0 = 1$ and $H_1 = 2q$, we can calculate all the others.
Simulating two-dimensional polycrystals
Posted by: christian in Featured on frontpage on 31 Mar 2019

The following code simulates (very approximately) the growth of a polycrystal from a number of seeds. Atoms are added to the crystal lattice of each of the resulting grains until no more will fit, creating realistic-looking boundaries where two grains meet.
Breeding tritium for a fusion reactor
Posted by: christian on 9 Jan 2019
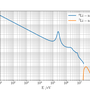
The most feasible nuclear reaction for a "first-generation" fusion reaction is the one involving deuterium (D) and tritium (T): $$ \mathrm{D} + \mathrm{T} \rightarrow \alpha (3.5\;\mathrm{MeV}) + n (14.1\;\mathrm{MeV}) $$ Tritium is not a primary fuel and does not exist in significant quantities naturally since it decays with a half life of 12.3 years. It therefore has to be "bred" from a separate nuclear reaction. Most fusion reactor design concepts employ a lithium "blanket" surrounding the reaction vessel which absorbs the energetic fusion neutrons to produce tritium in such a reaction.
Wa-Tor World on a torus
Posted by: christian on 27 Dec 2018
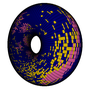
The population dynamics simulation known as Wa-Tor was described in a previous post. When carried out on a grid with periodic boundary conditions, the Wa-Tor "universe" is topologically equivalent to a torus, as depicted below using the code provided here.