Viewing posts by christian
Gyromotion of a charged particle in a magnetic field
Posted by: christian in Featured on frontpage on 11 Sep 2018
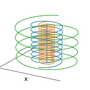
A charged particle of mass $m$ and charge $q$ moving with a velocity $\boldsymbol{v}$ in an an electric field $\boldsymbol{E}$ and a magnetic field $\boldsymbol{B}$ is subject to a Lorentz force, $\boldsymbol{F}$, given by
$$
\boldsymbol{F} = q(\boldsymbol{E} + \boldsymbol{v}\times\boldsymbol{B}).
$$
The equation of motion for a single particle is therefore given by Newton's second law as
$$
\boldsymbol{\ddot{r}} = \frac{q}{m}(\boldsymbol{E} + \boldsymbol{v}\times\boldsymbol{B}).
$$
Here we will consider a uniform magnetic field, $\boldsymbol{B} = (0,0,B)$ and zero electric field, $E=0$. In this case, the trajectory of the particle can be obtained by solving the equation of motion analytically, but here we integrate it numerically using SciPy's integrate.odeint method. Assuming the particle starts off with non-zero components of its velocity parallel ($v_\parallel$) and perpendicular ($v_\perp$) to the magnetic field, it moves in a helix, with radius given by
$$
\rho = \frac{mv_\perp}{|q|B},
$$
known as the Larmor or cyclotron radius (or gyroradius).
Rotating text onto a line in Matplotlib
Posted by: christian on 3 Sep 2018
Sometimes it is necessary to rotate a text annotation in a Matplotlib figure so that it is aligned with a line plotted on the figure Axes. Axes.annotation takes an argument, rotation, to allow a text label to be rotated, and a naive implementation might be as follows:
Types of plasma
Posted by: christian in Featured on frontpage on 2 Sep 2018
Two important parameters in plasma physics are the electron Debye length, $\lambda_{\mathrm{D}e}$, a measure of the distance over which charge-screening effects occur and deviations from quasi-neutrality are observed, and the number of paricles in a "Debye cube" (of side length $\lambda_{\mathrm{D}e}$), $N_\mathrm{D}$.
The Debye length
Posted by: christian on 21 Aug 2018
An important concept in plasma physics is the Debye length, which describes the screening of a charge's electrostatic potential due to the net effect of the interactions it undergoes with the other mobile charges (electrons and ions) in the system. It can be shown that, given a set of reasonable assumptions about the behaviour of charges in the plasma, the electric potential due to a "test charge", $q_\mathrm{T}$ is given by $$ \phi = \frac{q_\mathrm{T}}{4\pi\epsilon_0 r}\exp\left(-\frac{r}{\lambda_\mathrm{D}}\right), $$ where the electron Debye length, $$ \lambda_\mathrm{D} = \sqrt{\frac{\epsilon_0 T_e}{e^2n_0}}, $$ for an electron temperature $T_e$ expressed as an energy (i.e. $T_e = k_\mathrm{B}T_e'$ where $T_e'$ is in K) and number density $n_0$. Rigorous derivations, starting from Gauss' Law and solving the resulting Poisson equation with a Green's function are given elsewhere (e.g. Section 7.2.2. in J. P. Freidberg, Plasma Physics and Fusion Energy, CUP (2008)).
A simple colouring grid
Posted by: christian on 15 Aug 2018
Just a simple Python app to try out the TkInter interface to the Tk GUI toolkit and to keep my children occupied. It shows a window with a square grid of cells which can be coloured by selecting from a palette. Run with