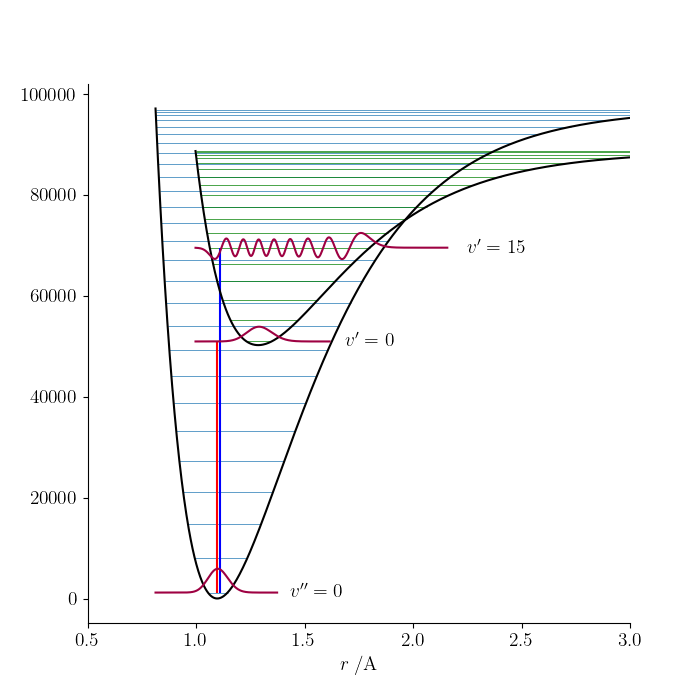
The Morse oscillator code introduced in a previous blog post can be used to visualize the vibronic transitions in a diatomic molecule by creating two Morse objects (one for each electronic state) and plotting their potential energy curves and energy levels on the same Matplotlib Axes object.

![enter image description here][1]{.fig}

import numpy as np
from matplotlib import rc
import matplotlib.pyplot as plt
from scipy.constants import h, c
from morse import Morse, FAC
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 14})
rc('text', usetex=True)

# Figure resolution and size in pixels.
DPI = 100
w, h = 700, 525
# The colour to plot wavefunctions in.
COLOUR1 = (0.6196, 0.0039, 0.2588, 1.0)

# Atom masses and ground state parameters for (14N)2.
mA = mB = 14.003074004
X_re = 1.09768e-10
X_Te = 0
X_we, X_wexe = 2358.57, 14.324

X = Morse(mA, mB, X_we, X_wexe, X_re, X_Te)
X.make_rgrid(rmax=3.e-10)
X.V = X.Vmorse(X.r)

# First excited electronic state parameters for (14N)2.
A_re = 1.2866e-10
A_Te = 50203.6
A_we, A_wexe = 1460.64, 13.87
A = Morse(mA, mB, A_we, A_wexe, A_re, A_Te)

fig, ax = plt.subplots(figsize=(w/DPI, w/DPI), dpi=DPI)
# Plot the ground state potential energy curve and vibrational energy levels.
X.plot_V(ax, color='k')
X.draw_Elines(range(0, X.vmax, 3), ax, lw=0.5)
# Draw and label the ground state vibrational wavefunction.
X.plot_psi([0], ax, scaling=4, color=COLOUR1)
X.label_levels([0], ax, [r"$v''=0$"])

# Plot the excited state potential energy curve and vibrational energy levels.
A.plot_V(ax, color='k')
A.draw_Elines(range(0, A.vmax, 3), ax, lw=0.5, color='g')
# Draw and label the excited state vibrational wavefunctions for v=0 and v=15.
A.plot_psi([0, 15], ax, scaling=4, color=COLOUR1)
A.label_levels([0, 15], ax, [r"$v'=0$", r"$v'=15$"])

# Some figure labelling and tidying.
ax.set_xlabel(r'$r \;/ \mathrm{\AA}$')
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

# Indicate a couple of transitions.
Epp = X.Emorse(0, 'cm-1', include_Te=True)
Ep = A.Emorse(0, 'cm-1', include_Te=True)
ax.vlines(X.re*1.e10, Epp, Ep, color='r')
Ep = A.Emorse(15, 'cm-1', include_Te=True)
ax.vlines(X.re*1.e10*1.01, Epp, Ep, color='b')
ax.set_xlim(0.5, 3)

plt.savefig('morse-vibronic.png', dpi=DPI)
plt.show()

There are a couple of changes to the original code, which are included in the updated version of morse.py here:

import numpy as np
from scipy.constants import h, hbar, c, u
from scipy.special import factorial
from scipy.special import genlaguerre, gamma

# Factor for conversion from cm-1 to J
FAC = 100 * h * c

class Morse:
    """A class representing the Morse oscillator model of a diatomic."""

    def __init__(self, mA, mB, we, wexe, re, Te):
        """Initialize the Morse model for a diatomic molecule.

        mA, mB are the atom masses (atomic mass units).
        we, wexe are the Morse parameters (cm-1).
        re is the equilibrium bond length (m).
        Te is the electronic energy (minimum of the potential well; origin
            of the vibrational state energies).

        """

        self.mA, self.mB = mA, mB
        self.mu = mA*mB/(mA+mB) * u
        self.we, self.wexe = we, wexe
        self.re = re
        self.Te = Te

        self.De = we**2 / 4 / wexe * FAC
        self.ke = (2 * np.pi * c * 100 * we)**2 * self.mu
        #  Morse parameters, a and lambda.
        self.a = self.calc_a()
        self.lam = np.sqrt(2 * self.mu * self.De) / self.a / hbar
        # Maximum vibrational quantum number.
        self.vmax = int(np.floor(self.lam - 0.5))

        self.make_rgrid()
        self.V = self.Vmorse(self.r)

    def make_rgrid(self, n=1000, rmin=None, rmax=None, retstep=False):
        """Make a suitable grid of internuclear separations."""

        self.rmin, self.rmax = rmin, rmax
        if rmin is None:
            # minimum r where V(r)=De on repulsive edge
            self.rmin = self.re - np.log(2) / self.a
        if rmax is None:
            # maximum r where V(r)=f.De
            f = 0.999
            self.rmax = self.re - np.log(1-f)/self.a
        self.r, self.dr = np.linspace(self.rmin, self.rmax, n,
                                      retstep=True)
        if retstep:
            return self.r, self.dr
        return self.r

    def calc_a(self):
        """Calculate the Morse parameter, a.

        Returns the Morse parameter, a, from the equilibrium
        vibrational wavenumber, we in cm-1, and the dissociation
        energy, De in J.

        """

        return (self.we * np.sqrt(2 * self.mu/self.De) * np.pi *
                c * 100)

    def Vmorse(self, r):
        """Calculate the Morse potential, V(r).

        Returns the Morse potential at r (in m) for parameters De
        (in J), a (in m-1) and re (in m).

        """

        return self.De * (1 - np.exp(-self.a*(r - self.re)))**2

    def Emorse(self, v, units='J', include_Te=False):
        """Calculate the energy of a Morse oscillator in state v.

        Returns the energy of a Morse oscillator parameterized by
        equilibrium vibrational frequency we and anharmonicity
        constant, wexe (both in cm-1).

        """
        vphalf = v + 0.5
        E = self.we * vphalf - self.wexe * vphalf**2
        if include_Te:
            E += self.Te
        if units == 'cm-1':
            return E
        elif units == 'J':
            return E * FAC
        raise ValueError('unrecognised units "{}" in Emorse'.format(units))

    def calc_turning_pts(self, E):
        """Calculate the classical turning points at energy E.

        Returns rm and rp, the classical turning points of the Morse
        oscillator at energy E (provided in J). rm < rp.

        """

        b = np.sqrt(E / self.De)
        return (self.re - np.log(1+b) / self.a,
                self.re - np.log(1-b) / self.a)

    def calc_psi(self, v, r=None, normed=True, psi_max=1):
        """Calculates the Morse oscillator wavefunction, psi_v.

        Returns the Morse oscillator wavefunction at vibrational
        quantum number v. The returned function is "normalized" to
        give peak value psi_max.

        """

        if r is None:
            r = self.r
        z = 2 * self.lam * np.exp(-self.a*(r - self.re))
        alpha = 2*(self.lam - v) - 1
        psi = (z**(self.lam-v-0.5) * np.exp(-z/2) *
               genlaguerre(v, alpha)(z))
        psi *= psi_max / np.max(psi)
        return psi

    def calc_psi_z(self, v, z):
        alpha = 2*(self.lam - v) - 1
        psi = (z**(self.lam-v-0.5) * np.exp(-z/2) *
               genlaguerre(v, alpha)(z))
        Nv = np.sqrt(factorial(v) * (2*self.lam - 2*v - 1) /
                     gamma(2*self.lam - v))
        return Nv * psi

    def plot_V(self, ax, **kwargs):
        """Plot the Morse potential on Axes ax."""

        ax.plot(self.r*1.e10, self.V / FAC + self.Te, **kwargs)

    def get_vmax(self):
        """Return the maximum vibrational quantum number."""

        return int(self.we / 2 / self.wexe - 0.5)

    def draw_Elines(self, vlist, ax, **kwargs):
        """Draw lines on Axes ax representing the energy level(s) in vlist."""

        if isinstance(vlist, int):
            vlist = [vlist]
        for v in vlist:
            E = self.Emorse(v)
            rm, rp = self.calc_turning_pts(E)
            ax.hlines(E / FAC + self.Te, rm*1.e10, rp*1e10, **kwargs)

    def label_levels(self, vlist, ax, labels=None):
        if isinstance(vlist, int):
            vlist = [vlist]
        if labels is None:
            labels = [r'$v={}$'.format(v) for v in vlist]

        for i, v in enumerate(vlist):
            E = self.Emorse(v)
            rm, rp = self.calc_turning_pts(E)
            ax.text(s=labels[i], x=rp*1e10*1.25,
                    y=E / FAC + self.Te, va='center')

    def plot_psi(self, vlist, ax, r_plot=None, scaling=1, **kwargs):
        """Plot the Morse wavefunction(s) in vlist on Axes ax."""
        if isinstance(vlist, int):
            vlist = [vlist]
        for v in vlist:
            E = self.Emorse(v)
            if r_plot is None:
                rm, rp = self.calc_turning_pts(E)
                x = self.r[self.r