Depicting a torus as an SVG image
Posted on 30 November 2018
SVG may not be the most obvious choice for depicting a 3-D object, but with some care over the perspective and ordering of the plotted points, it can be done.
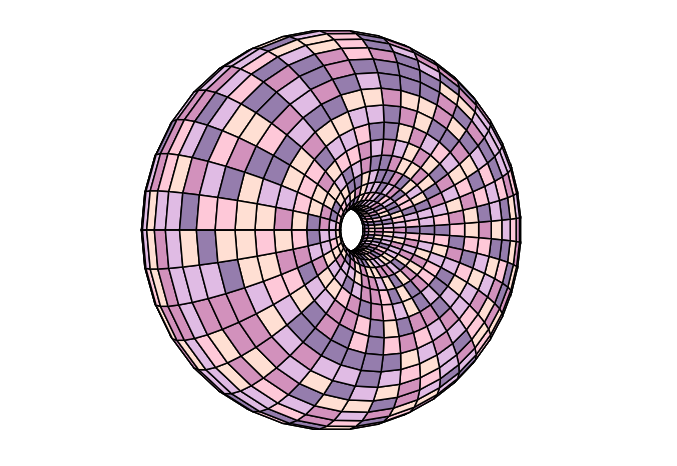
The code is below and relies on a single import for the colour scheme, palettes.py, also below.
import numpy as np
from palettes import colour_funcs
# The major and minor radius of the torus.
c, a = 1.5, 1.2
# Pick a colour scheme from the get_colours dictionary
palette = 'pastels'
# Image dimensions and scaling factors from torus units to image units.
width, height = 800, 600
scalex, scaley = 140, 140
# Tait-Bryan angles for intrinsic rotation of the figure.
alpha, beta, gamma = 90, 25, 0
# Camera position, C, and projection plane position, E (relative to C).
cx, cy, cz = 0, 6, 0
ex, ey, ez = 0, 3, 0
# Number of quads per 2.pi radians around each angular coordinate.
ntheta, nphi = 40, 40
def preamble(fo):
"""The SVG preamble and styles."""
print('<?xml version="1.0" encoding="utf-8"?>\n'
'<svg xmlns="http://www.w3.org/2000/svg"\n' + ' '*5 +
'xmlns:xlink="http://www.w3.org/1999/xlink" width="{}" height="{}" >'
.format(width, height), file=fo)
print("""
<defs>
<style type="text/css"><![CDATA[""", file=fo)
print('path {stroke-width: 1.5px; stroke: #000;}', file=fo)
print("""]]></style>
</defs>""", file=fo)
def get_xyz(theta, phi):
"""Get the cartesian coordinates of a point on the torus."""
x = (c + a*np.cos(theta)) * np.cos(phi)
y = (c + a*np.cos(theta)) * np.sin(phi)
z = a * np.sin(theta)
return x, y, z
def rotate_xyz(xyz, alpha, beta, gamma):
"""Rotate the point(s) P=xyz by Rz(alpha)Ry(beta)Rx(gamma).P"""
alpha, beta, gamma = np.radians(alpha), np.radians(beta), np.radians(gamma)
ca, sa = np.cos(alpha), np.sin(alpha)
Rz = np.array(((1,0,0),(0,ca,-sa),(0,sa,ca)))
cb, sb = np.cos(beta), np.sin(beta)
Ry = np.array(((cb,0,sb),(0,1,0),(-sb,0,cb)))
cg, sg = np.cos(gamma), np.sin(gamma)
Rx = np.array(((cg,-sg,0),(sg,cg,0),(0,0,1)))
R = Rz @ Ry @ Rx
return xyz @ R.T
# Create a mesh of points on the two angular coordinates, theta and phi.
theta = np.linspace(0, 2.*np.pi, ntheta)
phi = np.linspace(0, 2.*np.pi, nphi)
theta, phi = np.meshgrid(theta, phi)
# Get the points on the mesh and rotate the torus by the specified angles.
x, y, z = get_xyz(theta, phi)
xyz = np.stack((x, y, z), axis=-1)
xyz = rotate_xyz(xyz, alpha, beta, gamma)
x, y, z = xyz.T
def apply_perspective(ax, ay, az):
"""
Simple perspective projection of point A onto display plane at E
as seen by camera at C.
"""
dx, dy, dz = ax-cx, ay-cy, az-cz
bx = ey/dy*dx + ex
bz = ey/dy*dz + ez
return bx, bz
bx, by = apply_perspective(x, y, z)
# Calculate the coordinates of the quads, and keep track of each quad's
# mean position in the y-axis (depth-axis) in ypos.
quads, ypos = [], []
# To look inside the torus, we may not want to draw it all. Specify the
# indexes of the phi coordinates of the quads to draw as j1, j2 here:
j1, j2 = nphi//2, nphi
j1, j2 = 0, nphi
ni, nj = ntheta, j2-j1
quads = np.empty((ni*nj,4,2))
for i in range(ntheta):
for j in range(j1, j2):
ip, jp = (i+1) % ntheta, (j+1) % nphi
ym = np.mean( (y[i,j], y[ip,j], y[ip,jp], y[i,jp]) )
quads[i*nj+j-j1] = ((bx[i,j], by[i,j]), (bx[ip,j], by[ip,j]),
(bx[ip,jp], by[ip,jp]), (bx[i,jp], by[i,jp]))
ypos.append(ym)
# Get the indexes of the quads sorted by their distance from the camera.
idy = np.argsort(ypos)
# Draw the torus as a SVG image.
get_colour = colour_funcs[palette]
with open('torus.svg', 'w') as fo:
preamble(fo)
for i in idy:
quad = quads[i] * (scalex, scaley) + (width/2, height/2)
p1,p2,p3,p4 = quad
colour = get_colour(i, idy)
print('<path d="M{},{} L{},{} L{},{} L{},{} Z" fill="{}"/>'.format(
p1[0],p1[1], p2[0],p2[1], p3[0],p3[1], p4[0],p4[1], colour),
file=fo)
print('</svg>', file=fo)
palettes.py:
# Some different colour schemes for our torus.
import random
def rgb_to_html(rgb):
return '#{:02x}{:02x}{:02x}'.format(*rgb)
pastel_colours = ['#e0bbe4', '#957dad', '#d291bc', '#fec8d8', '#ffdfd3']
elmer_colours = [[68,90,233], [112,0,128], [103,204,33], [217,17,29],
[228,151,200], [239,240,233], [23,16,16], [242,97,9], [251,236,21]]
for i, rgb in enumerate(elmer_colours):
elmer_colours[i] = rgb_to_html(rgb)
def depth_shaded(i,idy):
"""Map the ramp i=0->b onto a triangle i=0->1->0."""
b = len(idy)
r = b - abs(i - b/2)
rgb = (int(r/b*255),)*3
return rgb_to_html(rgb)
colour_funcs = {
'grey': lambda i, _: '#dddddd',
'pastels': lambda i, _: random.choice(pastel_colours),
'elmer': lambda i, _: random.choice(elmer_colours),
'depth shaded': depth_shaded,
}
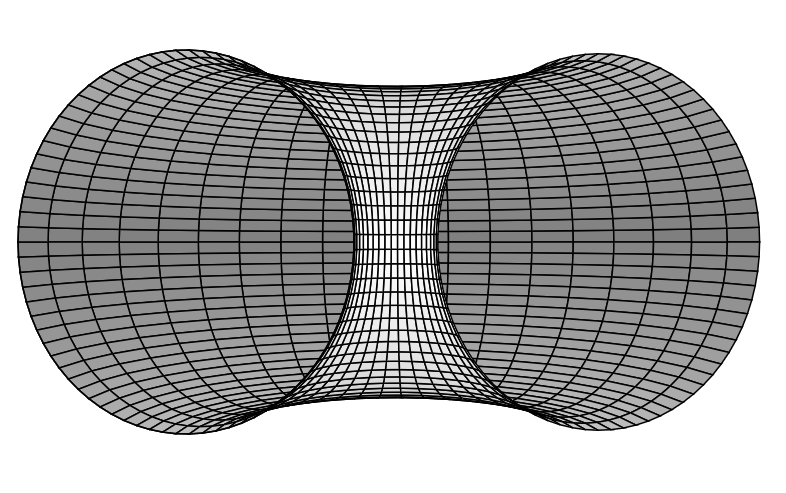
By changing the angular range of the coordinate $\phi$, one can look inside the torus:
Or, in Elmer colours:
