Posted by: christian on 19 Dec 2019
Piphilology comprises the creation and use of mnemonic techniques to remember a span of digits of the mathematical constant $\pi$. One famous technique, attributed to the physicist James Jeans uses the number of letters in each word of the sentence:
How I want a drink, alcoholic of course, after the heavy chapters involving quantum mechanics
The Python script below takes a text file on the command line and tries to find the longest sequence ("run") of words that could serve as a mnemonic. It turns out that random texts don't tend to contain mnemonics of any useful length, and a typical novel of a few hundred thousand words will likely not contain one of length longer than 5 words. For example, using the text of David Copperfield from Project Gutenberg:
$ python get_pi_mnemonic.py david-copperfield.txt
david-copperfield.txt contains 357732 words
898 runs of length 3 found:
"XIX I Look", "XXX A Loss", "Yet I have", "all I know", "had a sure", "her I dare", "not a rook", "yes I fear", ...
32 runs of length 4 found:
"III I Have a", "you I have a", "And I hope I", "man I have a", "her a turn I", "sir I said I", "sir I said I", "Yes I said I", ...
5 runs of length 5 found:
"and I made a cloak", "you I hope I shall", "was a lady I think", "now a mans a judge", "why I felt a vague"
The sixth digit of $\pi$ is 9 and there aren't that many common words with 9 letters (compared to those with 1 – 5 letters).
import sys
from math import pi, e
from collections import defaultdict
MIN_RUN_LENGTH = 3
PI_DIGITS = [int(d) for d in '3141592653589793238462643383279502884']
# Alternatively, the first 16 digits of e, the base of natural logarithms.
E_DIGITS = [int(d) for d in str(e) if d != '.']
# Read the text and clean it up, removing non-alphabetic characters but
# retaining spaces and replacing new lines with spaces.
text_filename = sys.argv[1]
with open(text_filename) as fi:
text = fi.read()
text = text.replace('\n', ' ')
text = ''.join([l for l in text if l.lower() in
'abcdefghijklmnopqrstuvwxyz åéüäèçáàøö'])
words = text.split()
nwords = len(words)
print(f'{text_filename} contains {nwords} words')
# the current "cursor" position within a run of words whose lengths
# are the digits of pi, and the starting position of the current run
# being studied.
j, k = 0, None
run = defaultdict(list)
for i in range(nwords):
word = words[i]
word_len = len(word)
if word_len == 10:
# Some mnemonics use 10-letter words to represent the digit 0.
word_len = 0
if word_len == PI_DIGITS[j]:
if j == 0:
# A new run to study: set the starting point.
k = i
j += 1
else:
# We're done with this run: add it to the run dict if it's
# at least MIN_RUN_LENGTH words long.
if j >= MIN_RUN_LENGTH:
jmax = j
kmax = k
run[j].append(' '.join(words[k:k+j]))
# Don't forget to reset the cursor position!
j = 0
def print_truncated_list(lst):
max_len = 8
truncated_list = lst[:max_len]
s = ', '.join(['"{}"'.format(run) for run in truncated_list])
if len(lst) > max_len:
s += ', ...'
print(s)
for run_len in sorted(run.keys()):
nruns = len(run[run_len])
print(f'{nruns} runs of length {run_len} found:')
print_truncated_list(run[run_len])
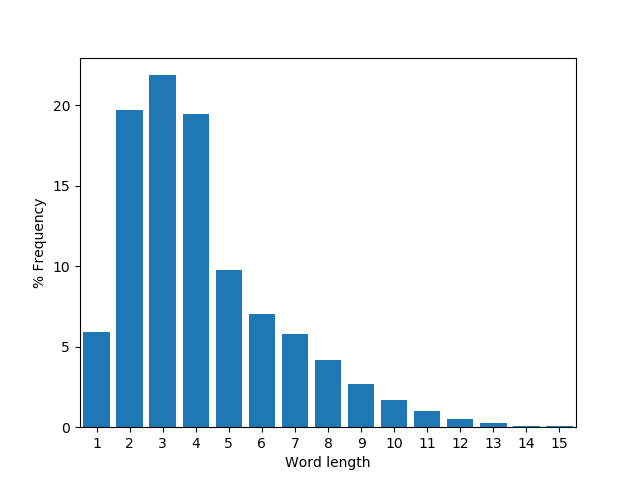
The word length frequencies for David Copperfield are plotted below using the following code. The expected number of $\pi$-mnemonic runs of each length for this text (assuming no correlation between the lengths of neighbouring words) are in broad agreement with those found:
1: n = 73612
2: n = 3710
3: n = 843
4: n = 47
5: n = 5
6: n < 1
import sys
from collections import Counter
import numpy as np
import matplotlib.pyplot as plt
PI_DIGITS = [int(d) for d in '3141592653589793238462643383279502884']
# Read the text and clean it up, removing non-alphabetic characters but
# retaining spaces and replacing new lines with spaces.
text_filename = sys.argv[1]
with open(text_filename) as fi:
text = fi.read()
text = text.replace('\n', ' ')
text = ''.join([l for l in text if l.lower() in
'abcdefghijklmnopqrstuvwxyz åéüäèçáàøö'])
words = text.split()
word_lens = [len(word) for word in words]
max_word_len = max(word_lens)
nwords = len(words)
print(f'{text_filename} contains {nwords} words')
# Get the word frequencies as percentage probabilities.
word_counts = Counter(word_lens)
f = np.array([0.] * (max_word_len+1))
for i in range(1, max_word_len+1):
f[i] = word_counts[i]/len(word_lens) * 100
p = f[:10] / 100
p[0] = f[10] / 100
nexpected = np.cumprod(p[PI_DIGITS[:-1]]) * (1-p[PI_DIGITS[1:]]) * nwords
for run_len, n in enumerate(nexpected, start=1):
if n < 1:
print(f'{run_len}: n < 1')
break
else:
print(f'{run_len}: n = {int(n)}')
plt.bar(range(0, max_word_len+1), f)
plt.xlim(0.5, 15.5)
plt.xticks(range(1,16))
plt.xlabel('Word length')
plt.ylabel('% Frequency')
plt.savefig('word_length_frequencies.png')
plt.show()
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
There are currently no comments
New Comment