Posted by: christian on 15 Nov 2019
The quadtree data structure is a convenient way to store the location of arbitrarily-distributed points in two-dimensional space. Quadtrees are often used in image processing and collision detection.
A quadtree works by recursively partitioning a two-dimensional space into regions represented by nodes which are allowed to hold a maximum number of distinct points (these could be particles in a molecular dynamics simulation, for example). In constructing the quadtree by inserting points, if a node becomes full, it acquires (becomes the parent of) four further nodes by splitting its region into (usually equally-sized) subregions. A new point falling within the original region can then be assigned to the appropriate subregion.
Quadtrees are used in algorithms that can, for example, identify particle collisions, locate all the points in a given area, or find the nearest point to a provided location. The structure of the quadtree means that points that are far from the area or point being considered do not need to be compared.
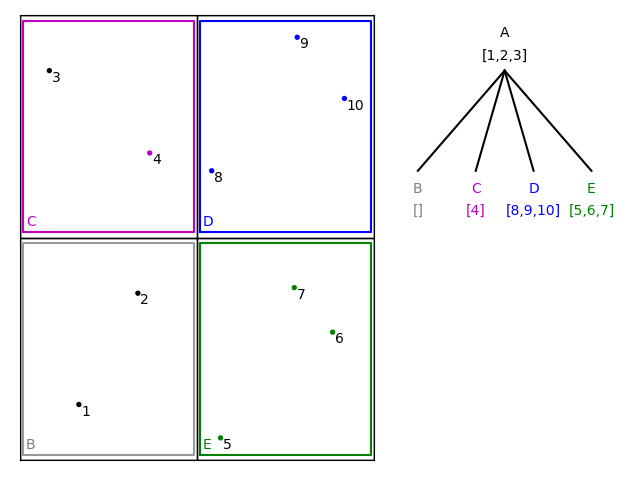
The following figures illustrate the working of a quadtree with a maximum number of 3 items per node.
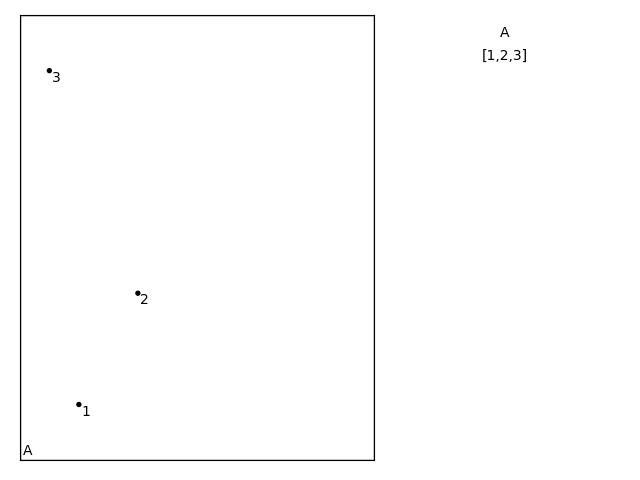
Initially, the root node, A, may be filled with three items:
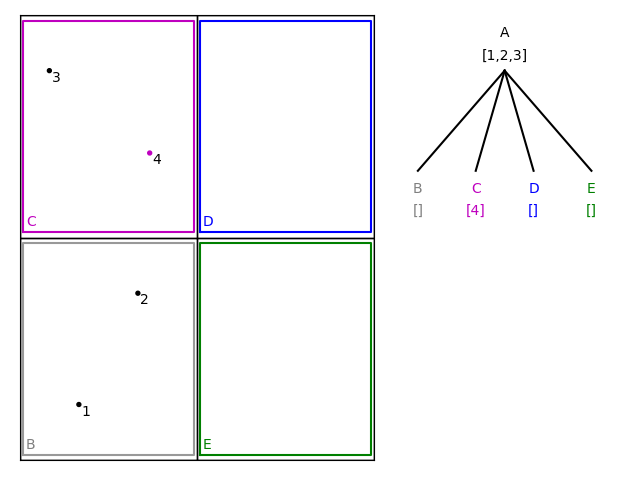
Adding a further item must cause the node to branch, creating four new child nodes, B–E. The location of the item means it is placed in node C:
The next three items happen to end up in node E, which can hold them without branching:
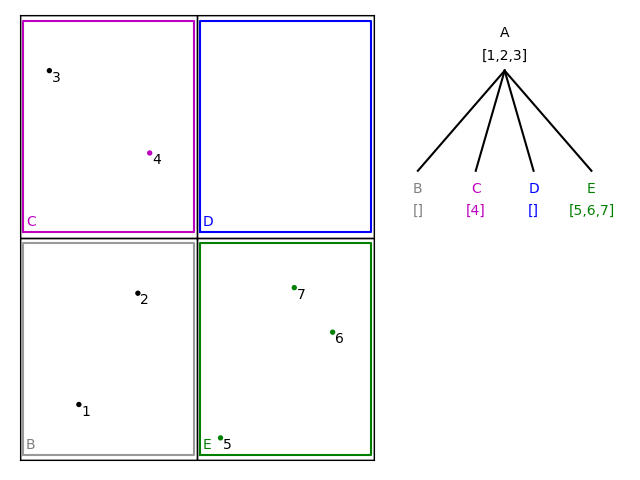
Similarly, the next three happen to fall into node D:
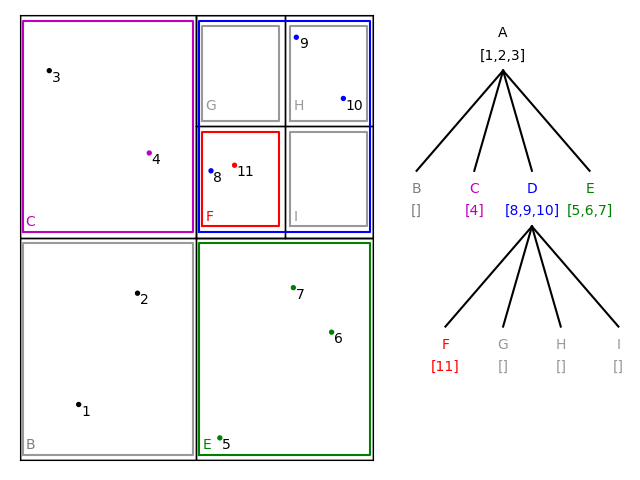
The 11th point also falls into the domain of node D, which must branch into four new nodes, F–I. The point is assigned to node F:
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
Artem 3 years ago
Hi folks! This is really interesting, short but good explanation of quadtree. I was looking for such an explanation and I want to use this algorithm and data structure for fast image matching. Thanks christian.
Link | ReplyNew Comment