Posted by: christian on 21 May 2017
A very simple diffusion simulation can be constructed in two dimensions by following the positions of a number of "particles" which all start off at the centre of a grid of cells. Time is assumed to progress in a series of "ticks": at each tick, each particle's position changes at random by $-1$, $0$, or $+1$ cells in each of the $x$ and $y$ directions.
Over time, the initial spike in particle density spreads out in the grid. The simulation is only a qualitative approximation to real diffusion because of the nine different movements a particle can make, one involves the particle not moving at all (i.e. a displacement of $(0,0)$) and the distances moved in the other eight are not all the same (compare, e.g. $(+1,0)$ and $(+1,+1)$).
But the result is pleasing enough.
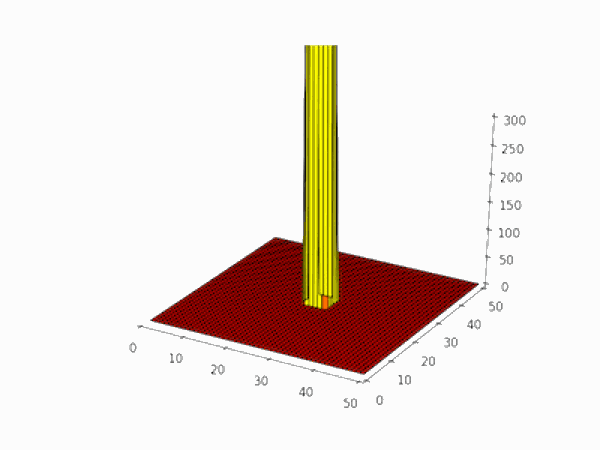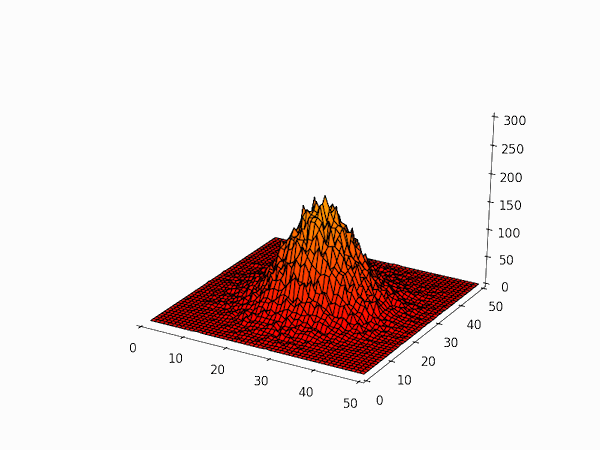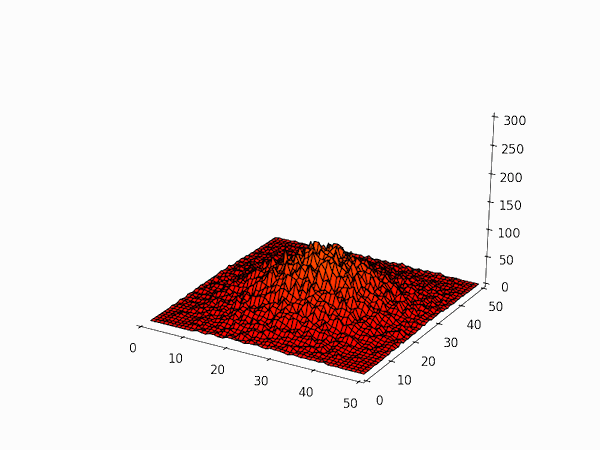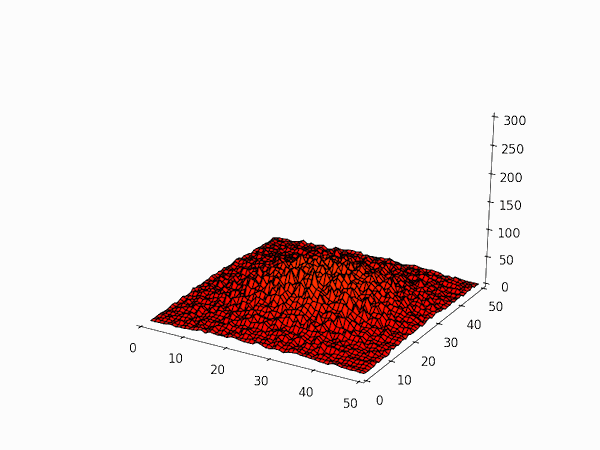
Here is the code used to generate the frames of the above animation. They can be put together into a gif with e.g. ImageMagick's convert utility.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import colors
# (Square) grid side length.
m = 50
# Maximum numbter of iterations.
nitmax = 200
# Number of particles in the simulation.
nparticles = 50000
# Output a frame (plot image) every nevery iterations.
nevery = 2
# Constant maximum value of z-axis value for plots.
zmax = 300
# Create the 3D figure object.
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# We'll need a meshgrid to plot the surface: this is X, Y.
x = y = np.linspace(1,m,m)
X, Y = np.meshgrid(x, y)
# vmin, vmax set the minimum and maximum values for the colormap. This is to
# be fixed for all plots, so define a suitable norm.
vmin, vmax = 0, zmax
norm = colors.Normalize(vmin=vmin, vmax=vmax)
# Initialize the location of all the particles to the centre of the grid.
locs = np.ones((nparticles, 2), dtype=int) * m//2
# Iterate for nitmax cycles.
for j in range(nitmax):
# Update the particles' locations at random. Particles move at random to
# an adjacent grid cell. We're going to be pretty relaxed about the ~11%
# probability that a particle doesn't move at all (displacement of (0,0)).
locs += np.random.randint(-1, 2, locs.shape)
if not (j+1) % nevery:
# Create an updated grid and plot it.
grid = np.zeros((m, m))
for i in range(nparticles):
x, y = locs[i]
# Add a particle to the grid if it is actually on the grid!
if 0 <= x < m and 0 <= y < m:
grid[x, y] += 1
print(j+1,'/',nitmax)
# Now clear the Axes of any previous plot and make a new surface plot.
ax.clear()
ax.plot_surface(X, Y, grid, rstride=1, cstride=1, cmap=plt.cm.autumn,
linewidth=1, vmin=vmin, vmax=vmax, norm=norm)
ax.set_zlim(0, zmax)
# Save to 'diff-000.png', 'diff-001.png', ...
plt.savefig('diff-{:03d}.png'.format(j//nevery))
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
amirach SAFAE 1 year, 8 months ago
hello please if someone can explaine to me this programm ?
Link | ReplyNew Comment