Posted by: christian on 30 Nov 2020
Natural uranium consists largely of two isotopes, $\mathrm{^{235}U}$ and $\mathrm{^{238}U}$. The less-abundant (0.72%) isotope, $\mathrm{^{235}U}$ , is important for nuclear reactors and weapons because it is the only isotope existing in nature to any appreciable extent that can sustain a fission chain reaction (that is, it is fissile).
For many purposes, natural uranium must be enriched in $\mathrm{^{235}U}$ to be used in reactors and weapons. For most power reactors, low-enriched uranium (LEU) of 3% – 5% is used; research reactors typically use high-assay LEU (HALEU) of 5 – 20% $\mathrm{^{235}U}$; naval reactors and some designs of fast-neutron reactor use highly enriched uranium (with greater than 20% $\mathrm{^{235}U}$); uranium enriched by 85% or more is used in nuclear weapon primaries and known as "weapons-grade" uranium.
Several enrichment processes have been demonstrated experimentally but the two deployed commercially are the gaseous diffusion process and the more efficient centrifuge process. Atomic vapor laser isotope separation (AVLIS) and similar technologies have also shown promise.
The capacity of enrichment plants is measured in terms of separative work units (SWU). The SWU is not a unit of energy, but rather expresses the amount of effort involved in enriching an amount of uranium from one $\mathrm{^{235}U}$ concentration (the feed assay) to another (product assay), leaving a depleted residue with a lower $\mathrm{^{235}U}$ concentration (the tails assay). It is defined as $$ SWU = W = PV(x_\mathrm{P}) + TV(x_\mathrm{T}) - FV(x_\mathrm{F}), \quad \mathrm{where}\;V(x) = (1-2x)\ln\left(\frac{1-x}{x}\right) $$ is the value function, a thermodynamic intensive quantity which expresses the energy input required to decrease the entropy of the sample in changing its composition and is defined so that the SWU is independent of concentration. Appendix A in Whitley, Rev. Mod. Phys. 56, 41 (1984) has more details of the derivation of $V(x)$. Here, $F$, $P$ and $T$ are the masses of the feed, product and tail uranium, respectively, and $x_\mathrm{F}$, $x_\mathrm{P}$, and $x_\mathrm{T}$ are their fractional $\mathrm{^{235}U}$ concentrations. The SWU formally has units of mass (kg): it increases in proportion to the amount of uranium to be processed.
For a fixed amount of feed uranium, $F$, with known assay, $x_\mathrm{F}$, the target product assay, $x_\mathrm{P}$ is obtained by enrichment, leaving a tails assay, $x_\mathrm{T}$, which could be chosen to minimize the cost function per kg of product, $$ J = \frac{L_\mathrm{F}F + L_\mathrm{SWU}W}{P}, $$ where $L_\mathrm{F}$ is the unit (per kg) cost of the feed uranium and $L_\mathrm{SWU}$ is the cost of each kg separative work.
$J$ turns out to be much more sensitive to the relative values of $L_\mathrm{F}$ and $L_\mathrm{SWU}$ and to $x_\mathrm{F}$ than to $x_\mathrm{P}$. The optimum tails assay, $x_\mathrm{T}$ is determined to be 0.3% by the code below, assuming realistic values of $L_\mathrm{F}$ = USD 100 / kg, $L_\mathrm{SWU}$ = USD 200 / kg, and natural uranium.
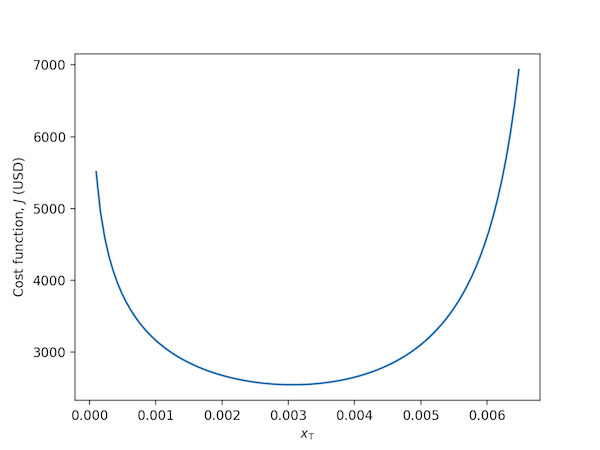
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
def V(x):
"""The separation value function for assay x."""
return (1 - 2*x) * np.log((1 - x) / x)
def SWU(F, xF, xP, xT):
"""Return the separative work for feed mass F.
xF, xP, and xT are the feed, product and tails assays, respectively.
"""
return F * ( (xF - xT) / (xP - xT) * V(xP)
+(xP - xF) / (xP - xT) * V(xT)
- V(xF)
)
def SWU_per_P(xF, xP, xT):
"""Return the SWU per product mass, P."""
return V(xP) + (xP-xF)/(xF-xT) * V(xT) - (xP-xT)/(xF-xT) * V(xF)
def cost_per_P(xT, xF, xP, LF, LSWU):
"""Return the cost per SWU.
xT, xF and xP are the tails, feed and product assays, respectively.
LF is the cost per unit mass of feed uranium, LSWU is the cost (in the
same currency) per unit mass of separative work, SWU.
"""
return LF * (xP-xT)/(xF-xT) + LSWU * SWU_per_P(xF, xP, xT)
# Feed assay is the natural abundance of U-235.
xF = 7.2e-3
# cost per kg of feed uranium, cost per kgSWU, in USD.
LF, LSWU = 100, 200
# Target product assay: the cost function is not very sensitive to xP.
xP = 0.05
# Target tails assays, xT: 0 < xT < xF.
xT = np.linspace(1e-4, xF*0.9, 100)
plt.plot(xT, cost_per_P(xT, xF, xP, LF, LSWU))
plt.xlabel('$x_\mathrm{T}$')
plt.ylabel('Cost function, $J$ (USD)')
plt.show()
# Minimize the cost function as a function of tails assay.
res = minimize(cost_per_P, [5.e-4], args=(xF, xP, LF, LSWU),
method='Nelder-Mead')
print('Optimum xT =', res.x[0])
Output:
Optimum xT = 0.0030625000000000092
Now consider the separative work per ton of feed uranium as a function of the desired product assay, $x_\mathrm{P}$:
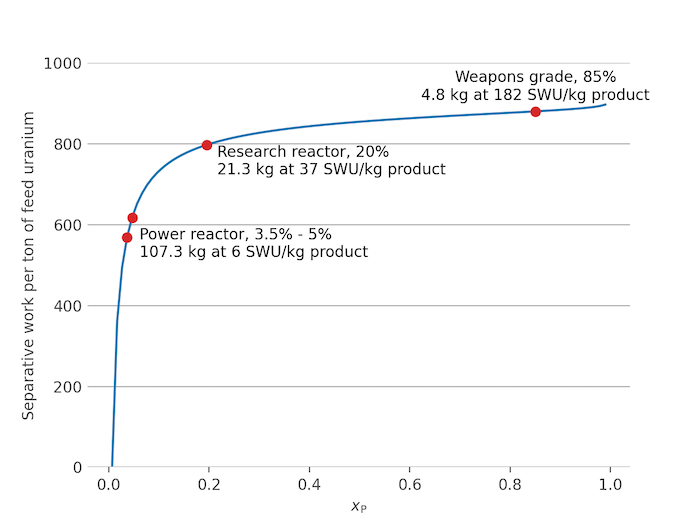
The above plot demonstrates why enrichment facilities are such a proliferation concern: the relative extra effort involved in generating >85% enriched uranium for weapons purposes is small compared to the effort to enrich by only, say, 20% for a research reactor.
The code generating this plot is below.
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
GREY = '#444444'
def V(x):
"""The separation value function for assay x."""
return (1 - 2*x) * np.log((1 - x) / x)
def SWU(F, xF, xP, xT):
"""Return the separative work for feed mass F.
xF, xP, and xT are the feed, product and tails assays, respectively.
"""
return F * ( (xF - xT) / (xP - xT) * V(xP)
+(xP - xF) / (xP - xT) * V(xT)
- V(xF)
)
def SWU_per_P(xF, xP, xT):
"""Return the SWU per product mass, P."""
return V(xP) + (xP-xF)/(xF-xT) * V(xT) - (xP-xT)/(xF-xT) * V(xF)
# Feed uranium mass, kg
F = 1000
# Feed assay is the natural abundance of U-235.
xF = 7.11e-3
# Optimum tails assay, 0.3%
xT = 0.003
# Target product assays: from just above natural abundance to 99%.
xP = np.linspace(xF*1.01, 0.99, 100)
# Product mass, tails mass
P = F * (xF - xT) / (xP - xT)
T = F - P
# Separative work per ton of feed uranium.
W_per_ton_F = SWU(F, xF, xP, xT) / F * 1000
# Separative work per ton of enriched product uranium.
W_per_kg_P = SWU(F, xF, xP, xT) / P
plt.plot(xP, W_per_ton_F)
plt.xlabel('$x_\mathrm{P}$')
plt.ylabel('Separative work per ton of feed uranium')
def find_nearest(arr, val):
"""Return the index of the value nearest to val in arr."""
idx = (np.abs(arr - val)).argmin()
return idx
# Plot some representative points on the SWU plot.
idx = find_nearest(xP, 0.2)
plt.plot(xP[idx], W_per_ton_F[idx], 'o', color='tab:red')
plt.text(xP[idx] + 0.02, W_per_ton_F[idx],
'Research reactor, 20%\n{:.1f} kg at {:.0f} SWU/kg product'
.format(P[idx], SWU_per_P(xF, xP[idx], xT)),
va='top'
)
idx = find_nearest(xP, 0.85)
plt.plot(xP[idx], W_per_ton_F[idx], 'o', color='tab:red')
plt.text(xP[idx], W_per_ton_F[idx] + 20,
'Weapons grade, 85%\n{:.1f} kg at {:.0f} SWU/kg product'
.format(P[idx], SWU_per_P(xF, xP[idx], xT)),
va='bottom', ha='center'
)
idx = (xP >= 0.035) & (xP <= 0.05)
x, y = xP[idx], W_per_ton_F[idx]
plt.plot(x, y, 'o', color='tab:red')
x, y, Pbar = np.mean(x), np.mean(y), np.mean(P[idx])
plt.text(x + 0.02, y,
'Power reactor, 3.5% - 5%\n{:.1f} kg at {:.0f} SWU/kg product'
.format(Pbar, SWU_per_P(xF, x, xT)),
va='top'
)
# Tidy up.
plt.ylim(0, 1000)
plt.box(on=None)
ax = plt.gca()
ax.yaxis.grid()
ax.tick_params(axis='x', colors=GREY)
ax.tick_params(axis='y', colors=GREY, length=0)
ax.xaxis.label.set_color(GREY)
ax.yaxis.label.set_color(GREY)
plt.show()
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
There are currently no comments
New Comment