Surface-to-volume ratios of some solid shapes

Posted by: christian on 27 Nov 2020

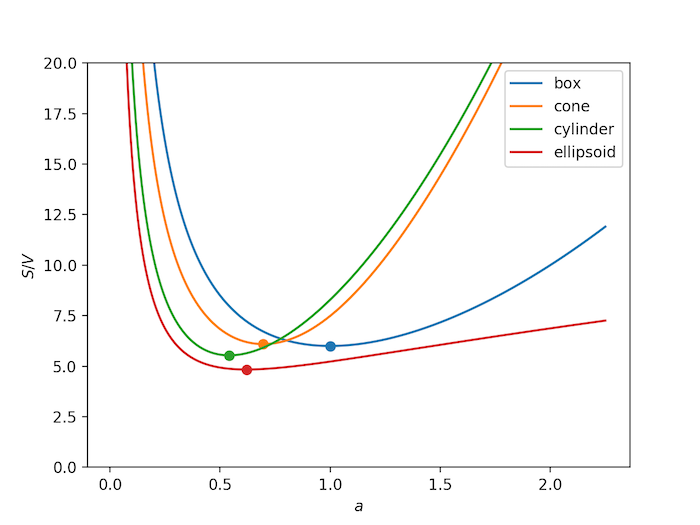
The shape with the minimum surface-to-volume ratio is the sphere. The code below plots this ratio for a variety of shapes as a function of a characteristic length:

Rectangular box of length $b$ with square cross section of area $a^2$

$$ S = 2a^2 + 4ab, \quad V = a^2b \Rightarrow b = \frac{b}{a^2}. $$ The minimum value of $S/V$ is realised for $a=b$ (a cube).

Right cone with height $h$ and maximum radius $a$

$$ S = 2\pi a ^2 + \pi a \sqrt{a^2 + h^2}, \quad V = \frac{1}{3}\pi a^2h \quad \Rightarrow h = \frac{3V}{\pi a^2}. $$

Right cylinder with height $h$ and radius $a$

$$ S = 2\pi a^2 + 2\pi a h, V = \pi a^2h \Rightarrow h = \frac{V}{\pi a^2} $$

Ellipsoid with semi-principal axes $a, b=c$

Despite the fact that the surface area of an ellipsoid of revolution may be expressed in terms of elementary functions, here we use the simple approximate formula, where $p=1.6075$, which has an error no greater than about 1%. $$ S \approx 4\pi \sqrt[p]{\frac{a^pb^p + a^pc^p + b^pc^p}{3}}, \quad V = \frac{4}{3}\pi abc \Rightarrow b = c = \sqrt{\frac{3V}{4\pi a}} $$ The minimum value of $S/V = 0.620$ occurs for $a=b=c$ (a sphere).

surface-to-volume ratios for some shapes

import numpy as np
import matplotlib.pyplot as plt

# Use a fixed volume of 1 somethings-cubed.
V = 1
# Grid of characteristic length values (e.g. side length, radius, ...)
a = np.linspace(0.01, 2.25, 1000)

def get_mins(sv):
    """Determine the minimum value of sv and corresponding value of a."""
    imin = np.argmin(sv)
    return a[imin], sv[imin]

def sv_ratio_box(V):
    """Surface-to-volume ratio of a rectangular box."""
    S = 2*a**2 + 4*V / a
    amin = V**(1/3)
    sv_min = 6/amin
    return S/V, (amin, sv_min)

def sv_ratio_cone(V):
    """Surface-to-volume ratio of a right cone."""
    h = 3 * V / np.pi / a**2
    S = np.pi * a * (a + np.sqrt(a**2 + h**2))
    sv = S/V
    return sv, get_mins(sv)

def sv_ratio_cylinder(V):
    """Surface-to-volume ratio of a right cylinder."""
    h = V / np.pi / a**2
    S = 2 * np.pi * a * (a + h)
    sv = S / V
    return sv, get_mins(sv)

def sv_ratio_ellipsoid(V):
    """Approximate surface-to-volume ratio of an ellipsoid."""
    b = c = np.sqrt(3 * V / 4 / np.pi / a)
    # Use the approximate formula to avoid messy elliptical integrals.
    p = 1.6075
    num = (a*b)**p + (a*c)**p + (b*c)**p
    S = 4 * np.pi * (num / 3)**(1/p)
    sv = S/V
    return sv, get_mins(sv)

# A list of functions for calculating the surface-to-volume ratios.
funcs = [(s, globals()['sv_ratio_'+s]) for s in ('box', 'cone', 'cylinder', 'ellipsoid')]
# Plot our figure, with the minima, and label.
fig, ax = plt.subplots()
for shape, func in funcs:
    sv, (amin, sv_min) = func(V)
    line, = ax.plot(a, sv, label=shape)
    ax.plot(amin, sv_min, 'o', c=line.get_color())
    print('{}: amin = {:g}, (S/V)min = {:g}'.format(shape, amin, sv_min))

ax.set_ylim(0, 20)
ax.set_xlabel('$a$')
ax.set_ylabel('$S/V$')
plt.legend()
plt.show()

Comments

Comments are pre-moderated. Please be patient and your comment will appear soon.

There are currently no comments