Penrose Tiling

Penrose Tiling 2: Implementation and Examples

Posted by christian on 26 May 2015

This article demonstrates the use of the Penrose tiling class described in the previous blog post.

The code described in this post is available under the GPL licence on GitHub.

Example 1: Inflation of a single tile

The Initial triangle is defined with the origin at the centre of its base:

An initial Robinson triangle for inflation to generate a Penrose tiling

This initial triangle is inflated for five generations. The default configuration is used for its appearance.

# example1.py
import math
from penrose import PenroseP3, BtileL, psi

# A simple example starting with a BL tile

scale = 100
tiling = PenroseP3(scale, ngen=5)

theta = 2*math.pi / 5
rot = math.cos(theta) + 1j*math.sin(theta)
A = -scale/2 + 0j
B = scale/2 * rot
C = scale/2 / psi + 0j
tiling.set_initial_tiles([BtileL(A, B, C)])
tiling.make_tiling()

tiling.write_svg('example1.svg')

P3 Penrose tiling: Example 1 — Example 1: A P3 Penrose tiling after inflation of the $B_L$ triangle five times

Example 2: A "sun" initialized by a semicircular arrangement of $B_S$ tiles.

The five initial B_S tiles are arranged as below, with their vertices calculated by successive rotations of the edge BA₁.

The initial configuration of five small Robinson triangles for inflation into a P3 Penrose tiling — The initial configuration of five $B_S$ tiles for inflation into a P3 Penrose tiling

# example2.py
import math
from penrose import PenroseP3, BtileS, BtileL

# A "sun"

scale = 100
config={'tile-opacity': 0.9, 'stroke-colour': '#800',
        'Stile-colour': '#f00', 'Ltile-colour': '#ff0'}
tiling = PenroseP3(scale*1.1, ngen=4, config=config)

theta = math.pi / 5
alpha = math.cos(theta)
rot = math.cos(theta) + 1j*math.sin(theta)
A1 = scale + 0.j
B = 0 + 0j
C1 = C2 = A1 * rot
A2 = A3 = C1 * rot
C3 = C4 = A3 * rot
A4 = A5 = C4 * rot
C5 = -A1
tiling.set_initial_tiles([BtileS(A1, B, C1), BtileS(A2, B, C2),
                          BtileS(A3, B, C3), BtileS(A4, B, C4),
                          BtileS(A5, B, C5)])
tiling.make_tiling()
tiling.write_svg('example2.svg')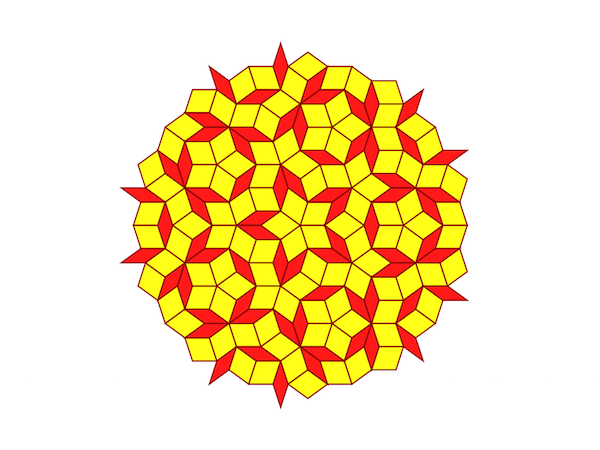

A P3 Penrose tiling after inflation of an initial arrangement of five small Robinson triangles — A P3 Penrose tiling after inflation of an initial arrangement of five $B_S$ triangles

Example 3: A star, including coloured arc lines

The five initial tiles are laid out as below, with the vertices p, q, r and s calculated by rotation of the edges AB₁ and AC₅.

The initial configuration of Robinson triangles for inflation into a star-shaped Penrose tiling

The completed star is rotated by 90 degrees so that one of its vertices points upwards and the arc and tile colours customized.

# example3.py
import math
from penrose import PenroseP3, BtileL, psi

# A star with five-fold symmetry

# The Golden ratio
phi = 1 / psi
scale = 100
config = {'draw-arcs': True,
          'Aarc-colour': '#ff5e25',
          'Carc-colour': 'none',
          'Stile-colour': '#090',
          'Ltile-colour': '#9f3',
          'rotate': math.pi/2}
tiling = PenroseP3(scale*2, ngen=5, config=config)

theta = 2*math.pi / 5
rot = math.cos(theta) + 1j*math.sin(theta)

B1 = scale
p = B1 * rot
q = p*rot

C5 = -scale * phi
r = C5 / rot
s = r / rot
A = [0]*5
B = [scale, p, p, q, q]
C = [s, s, r, r, C5]

tiling.set_initial_tiles([BtileL(*v) for v in zip(A, B, C)])
tiling.make_tiling()

tiling.write_svg('example3.svg')