Solution P8.2.6
The code below uses scipy.integrate.solve_ivp to solve the three coupled differential equations describing the concentrations of $\mathrm{O_2}$, $\mathrm{O}$ and $\mathrm{O_3}$ with time.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
# Reaction rate constants.
k1 = 3.e-12 # O2 + hv -> 2O (s-1)
k2 = 1.2e-33 # O2 + O + M -> O3 + M (cm6.molec-2.s-1)
k3 = 5.5e-4 # O3 + hv' -> O + O2 (s-1)
k4 = 6.9e-16 # O + O3 -> 2O2 (cm3.molec-1.s-1)
def deriv(t, c, M):
""" Return the d[X]/dt for each species."""
O2, O, O3 = c
dO2dt = -k1*O2 - k2*M*O*O2 + k3*O3 + 2*k4*O*O3
dOdt = 2*k1*O2 - k2*M*O*O2 + k3*O3 - k4*O*O3
dO3dt = k2*M*O*O2 - k3*O3 - k4*O*O3
return dO2dt, dOdt, dO3dt
# Total molecule concentration, M, and O2 concentration, cO2.
M = 9.e17
cO2 = 0.21*M
# Initial conditions for [O2], [O], [O3]
c0 = [cO2, 0, 0]
# Integrate the differential equations over a suitable time grid (s).
ti, tf = 0, 1.e8
# NB We need a solver that is robust to stiff ODEs.
soln = solve_ivp(deriv, (ti, tf), c0, args=(M,), method='LSODA')
t, c = soln.t, soln.y
# Steady-state approximation solution for comparison.
cO3ss = np.sqrt(k1 * k2 / k3 / k4 * M) * cO2
cOss = k3 * cO3ss / k2 / cO2 / M
print('Numerical values:\n[O] = {:g} molec/cm3, [O3] = {:g} molec/cm3'
.format(*c[1:,-1]))
print('Steady-state values:\n[O]ss = {:g} molec/cm3, [O3]ss = {:g} molec/cm3'
.format(cOss, cO3ss))
# Plot the evolution of [O3] and [O] with time
plt.plot(t,c[2], label=r'$\mathrm{[O_3]}$')
plt.plot(t,c[1], label=r'$\mathrm{[O]}$')
plt.yscale('log')
plt.ylim(1.e5, 1.e14)
plt.xlabel(r'$t\;/\mathrm{s}$')
plt.ylabel(r'$[\cdot\,]\;/\mathrm{molec\,cm^{-3}}$')
plt.legend()
plt.show()
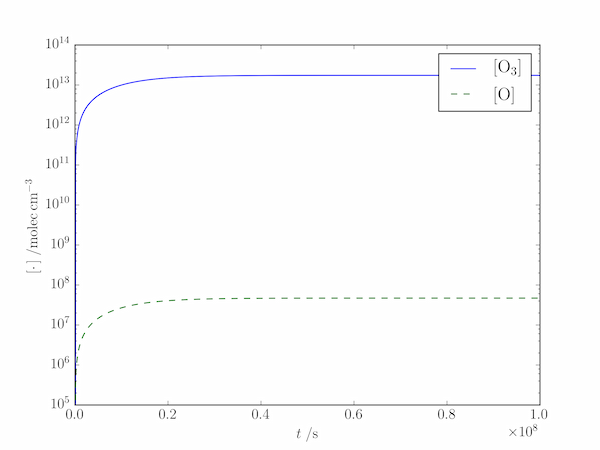
The output shows that the steady-state approximation works well at this altitude:
Numerical values:
[O] = 4.70561e+07 molec/cm3, [O3] = 1.74604e+13 molec/cm3
Steady-state values:
[O]ss = 4.7055e+07 molec/cm3, [O3]ss = 1.74634e+13 molec/cm3