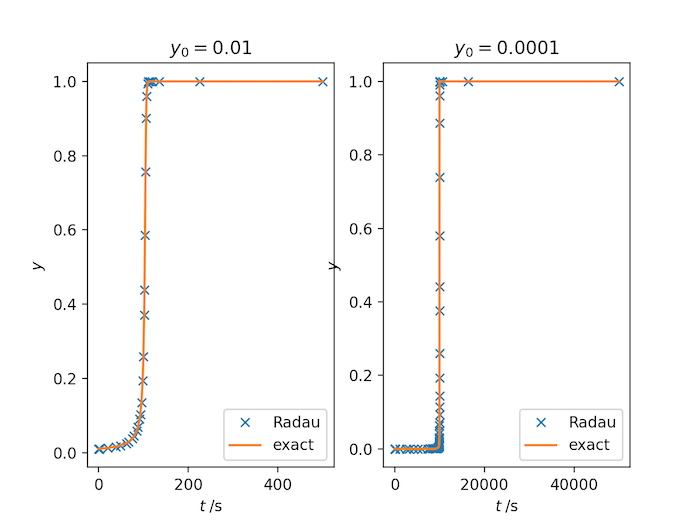
Solution P8.2.9
Here is one solution. The 'Radau' solver (an implicit Runge-Kutta method) is suitable, and requires 262 function evaluations for $y(0) = 0.01$ and 546 at $y(0) = 0.0001$.
import numpy as np
from scipy.integrate import solve_ivp
from scipy.special import lambertw
import matplotlib.pyplot as plt
method = 'Radau'
def solve_flame_eqn(alpha, beta, y0):
def dydt(t, y):
ydot = y**2 * (alpha - beta*y)
return ydot
t0, tf = 0, 5/y0
# Integrate the differential equation.
sol = solve_ivp(dydt, (t0, tf), [y0], method=method)
t, y = sol.t, sol.y[0]
print('alpha/beta = {}, y(0) = {}: nfev = {}'
.format(alpha/beta, y0, sol.nfev))
return t, y
def make_plot(ax, t, y):
a = alpha/beta/y0 - 1
yW = alpha / beta / (1 + lambertw(a * np.exp(a-alpha**2*t/beta)))
ax.plot(t, y, 'x', label=method)
ax.plot(t, yW, label='exact')
ax.set_xlabel(r'$t \;/\mathrm{s}$')
ax.set_ylabel(r'$y$')
ax.legend()
fig, axes = plt.subplots(nrows=1, ncols=2)
alpha, beta = 1, 1
y0 = 0.01
t, y = solve_flame_eqn(alpha, beta, y0)
make_plot(axes[0], t, y)
axes[0].set_title(r'$y_0 = 0.01$')
y0 = 1.e-4
t, y = solve_flame_eqn(alpha, beta, y0)
make_plot(axes[1], t, y)
axes[1].set_title(r'$y_0 = 0.0001$')
plt.show()