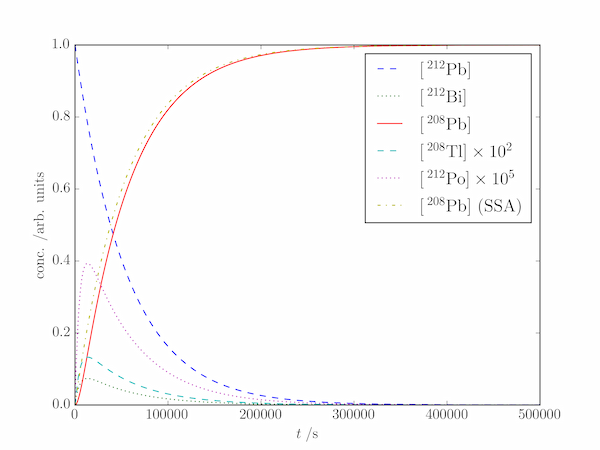
Solution P8.2.8
Although we could invoke the steady-state approximation (at least for $\mathrm{[^{208}Tl]}$ and $\mathrm{[^{212}Po]}$) to reduce the number of differential equations, the code below integrates them all.
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
species = ['212Pb', '212Bi', '208Tl', '212Po', '208Pb']
# The decay processes and their indexes in the list of rate coefficients, k
# 0: 212Pb -> 212Bi + beta-
# 1: 212Bi -> 208Tl + alpha
# 2: 212Bi -> 212Po + beta-
# 3: 208Tl -> 208Pb + beta-
# 4: 212Po -> 208Pb + alpha
k = [1.816e-05, 6.931e-05, 1.232e-4, 3.851e-3, 2.310]
def deriv(t, X):
""" Return dX/dt for each of the species. """
return (-k[0] * X[0], # 212Pb
k[0] * X[0] - k[1] * X[1] - k[2] * X[1], # 212Bi
k[1] * X[1] - k[3] * X[2], # 208Tl
k[2] * X[1] - k[4] * X[3], # 212Po
k[3] * X[2] + k[4] * X[3] # 208Pb
)
# Initial conditions: only 212Pb present
X0 = [1,0,0,0,0]
# Integrate the differential equations for tf secs
tf = 5.e5
soln = solve_ivp(deriv, (0, tf), X0, method='LSODA')
t = soln.t
X = soln.y
plt.plot(t, X[0], label=r'$[\,\mathrm{^{212}Pb}]$', c='k', ls='--')
plt.plot(t, X[1], label=r'$[\,\mathrm{^{212}Bi}]$', c='k', ls=':')
plt.plot(t, X[4], label=r'$[\,\mathrm{^{208}Pb}]$', c='k')
plt.plot(t, X[2]*1.e2, label=r'$[\,\mathrm{^{208}Tl}] \times 10^{2}$',
c='gray', ls='--')
plt.plot(t, X[3]*1.e5, label=r'$[\,\mathrm{^{212}Po}] \times 10^{5}$',
c='gray', ls=':')
Css = (1-np.exp(-k[0]*t)) # all intermediates in steady-state
plt.plot(t, Css, c='k', ls='-.', label=r'$[\,\mathrm{^{208}Pb}]$ (SSA)')
plt.legend()
plt.xlabel(r'$t\;/\mathrm{s}$')
plt.ylabel(r'conc. /arb. units')
plt.show()