Solution P8.1.4
Here is one solution.
import numpy as np
from scipy.special import ellipkinc, ellipeinc
def ellipsoid_surface(a, b, c):
# We must have a >= b >= c, so order the arguments
a, b, c = reversed(sorted([a,b,c]))
if a == c:
# The ellipsoid is a sphere
return 4 * np.pi * a**2
cosphi = c / a
phi = np.arccos(cosphi)
cosphi2 = cosphi ** 2
sinphi2 = 1 - cosphi2
k2 = a**2 * (b**2 - c**2) / b**2 / (a**2 - c**2)
# Round to 8 decimal places to avoid an unfortunate numerical instability
k2 = round(k2,8)
return 2 * np.pi * c**2 + 2 * np.pi * a * b / np.sin(phi)\
* (ellipkinc(phi,k2) * cosphi2 + ellipeinc(phi,k2) * sinphi2)
def ellipsoid_surface_approx(a, b, c):
# We must have a >= b >= c, so order the arguments
a, b, c = reversed(sorted([a,b,c]))
cosphi = c / a
phi = np.arccos(cosphi)
r = phi / np.sin(phi)
return 2 * np.pi * c**2 + 2 * np.pi * a * b * r * (1 - (b**2 - c**2)
/ 6 / b**2 * r**2 * (1 - (3*b**2 + 10*c**2)/56/b**2 * r**2))
# Fix a = 1 and construct an array of values for b = 0.02, 0.04, ... 0.98
a = 1
db = 0.02
nb = int((1 - 2*db)/db + 1)
bgrid = np.linspace(db, 1-db, nb)
# de will hold the relative error for different combinations of (b, c)
# de is symmetric, so only calculate for b >= c
de = np.zeros((nb,nb))
for i, b in enumerate(bgrid):
for j in range(0,i+1):
c = bgrid[j]
Sexact = ellipsoid_surface(a, b, c)
Sapprox = ellipsoid_surface_approx(a, b, c)
de[i,j] = np.abs(Sexact - Sapprox)/Sexact
# Fill in the symmetric upper triangle of the de array
de = de + de.T - np.diag(de.diagonal())
maxde = np.max(np.abs(de))
print('Maximum percentage error in approximation: {:.2f}'.format(maxde * 100))
import matplotlib.pyplot as plt
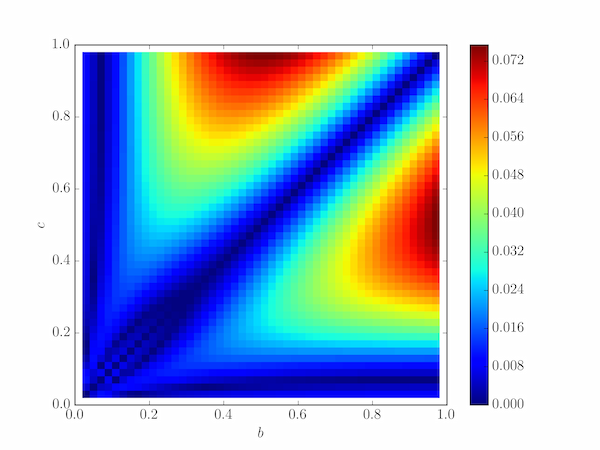
plt.pcolor(bgrid, bgrid, de)
plt.xlabel(r'$b$')
plt.ylabel(r'$c$')
plt.colorbar()
plt.show()
A couple of points about the above code should be explained. Firstly, the algorithm requires $a, b, c$ to satisfy $a \ge b \ge c$ so we order them that way and check that the ellipsoid isn't a sphere (the definition of k2 will run into problems if it is since its denominator will be zero).
There turns out to be a curious numerical instability in SciPy's implementation of the incomplete elliptic integrals for some particular exact combinations of $\phi$ and $k^2$, so we round k2 to 8 decimal places (more than enough) to skirt it.
To analyse the approximate ellipsoid surface area formula we need to investigate the results produce for different combinations of $a$, $b$ and $c$. There are really only two degrees of freedom here so we can pick one of them, $a$, to be anything we like and we choose $a=1$. Then we consider values of $b$ satisfying $0 < b < 1$, at some convenient resolution (steps of 0.02) and values of $c$ at the same resolution, with $b >= c$ (the volume clearly doesn't depent on which axis is called $b$ and which is called $c$). We can fill in the symmetric triangle of the difference array by adding it to the transpose of itself and subtracting the diagonal. The relative error is plotted below.