Solution P8.1.2
The code below uses the Bessel functions scipy.special.jn and jn_zeros. The function $J_1(x)/x$ is sometimes known as the jinc function (by comparison with the sinc function).
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jn, jn_zeros
fig = plt.figure()
ax = fig.add_subplot(111)
x = np.linspace(-10,10,100)
# The jinc, or "sombrero" function, J0(x)/x
jinc = lambda x: jn(1, x) / x
airy = (2 * jinc(x))**2
ax.plot(x,airy)
ax.set_xlabel('$x$')
ax.set_ylabel('$I(x)/I_0$')
plt.show()
# Aperture radius (mm), light wavelength (nm)
a, lam = 1.5, 500
# wavenumber (mm-1)
k = 2 * np.pi / (lam / 1.e6)
# First zero in J1(x)
x1 = jn_zeros(1, 1)[0]
theta1 = np.arcsin(x1 / k / a)
# Convert from radians to arcsec
theta1 = np.degrees(theta1) * 60 * 60
print('Maximum resolving power for pupil diameter {} mm at {} nm is {:.1f}'
' arcsec'.format(2*a, lam, theta1))
Output:
Maximum resolving power for pupil diameter 3.0 mm at 500 nm is 41.9 arcsec
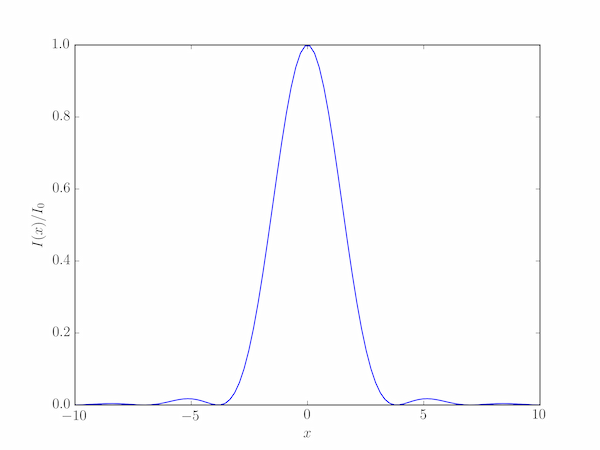
The reported maximum resolving power is about 42 arcsec.