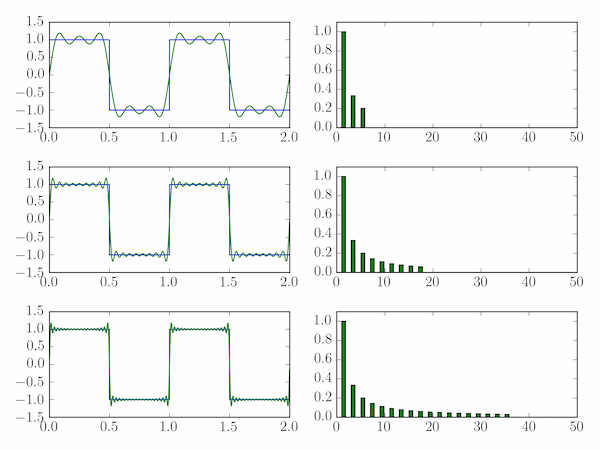
Solution P6.7.2
The three cases are handled in the code below.
import numpy as np
import matplotlib.pyplot as plt
n = 2048
T = 1
freq = 1 / T
duration = 2
t = np.arange(0, duration, duration/n)
f = np.ones(n)
f[(t >= T/2) & (t < T)] = -1
f[t >= T] = f[t < T]
def fourier_expansion(nterms):
fourier_square = np.zeros(n)
for k in range(1, nterms+1):
fac = 2 * k - 1
fourier_square += np.sin(2 * np.pi * fac * freq * t)/ fac
return 4 / np.pi * fourier_square
for i, nterms in enumerate((3, 9, 18)):
fourier_square = fourier_expansion(nterms)
F = (duration/n) / (4/np.pi) * np.abs(np.fft.rfft(fourier_square))
Fdft = (duration/n) / (4/np.pi) * np.abs(np.fft.rfft(f))
Ffreq = np.fft.rfftfreq(n, duration/n)
plt.subplot(3,2,i*2+1)
plt.plot(t,f)
plt.plot(t, fourier_square)
plt.ylim(-1.5, 1.5)
plt.subplot(3,2,(i+1)*2)
plt.bar(Ffreq, F, color='g')
plt.xlim(0,50)
plt.ylim(0,1.1)
plt.tight_layout()
plt.show()
The figure produced is shown below (Fourier expansion terms are illustrated on the right.)