Solution P6.6.4
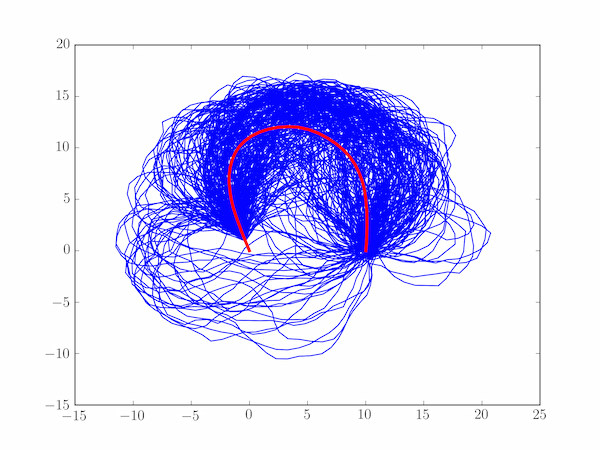
The main part of the program below consists of two loops: each time around the outer loop over the number of trials we reset $\phi_0$ and the array of path positions, pos and conduct the random walk over $n$ steps (the inner loop). If, after a walk, we are within one unit of the end position, B, we add that walk to the average, plot it, and increment the counter for completed walks, ngood. Finally, we divide our accumulated paths by ngood to find the average path and plot that.
import numpy as np
import matplotlib.pyplot as plt
# Random walk from a = (0,0) to b = (b, 0)
b = 10
# Set off each time at an angle phi0 from the a-b direction
phi0 = np.radians(110)
# Take a total of 40 steps
n = 40
# At each step, change phi by a random amount selected from a normal
# distribution with standard deviation sigma
sigma = np.radians(17)
# Conduct a total of ntrials walks
ntrials = 1000000
av = np.zeros((n, 2))
ngood = 0
for j in range(ntrials):
phi = phi0
pos = np.zeros((n, 2))
for i in range(1, n):
dx, dy = np.cos(phi), np.sin(phi)
pos[i] = pos[i-1] + (dx, dy)
phi += sigma * np.random.randn()
if np.hypot(b-pos[-1,0], pos[-1,1]) < 1.:
plt.plot(pos[:,0], pos[:,1], color='b')
av += pos
ngood += 1
print(j)
av /= ngood
plt.plot(av[:,0], av[:,1], lw=3, color='r')
plt.show()
A typical output is shown below.