Buffon's needle

Let a needle land randomly such that the smallest distance of its centre to the nearest line is $x$. Then the needle will cross the line if $x \le \frac{l}{2}\sin\theta$ as shown in the diagram below:

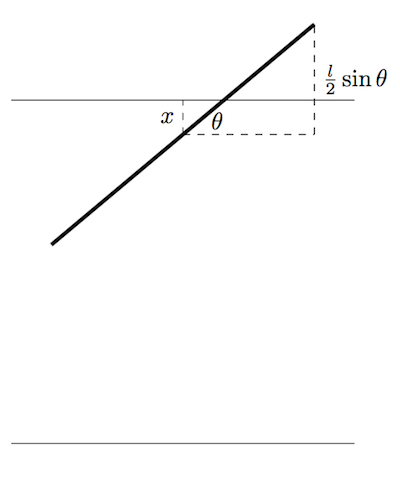
$\theta$ and $x$ ($0 \le \theta < \frac{\pi}{2}$, $0 \le x < \frac{d}{2}$) are independent random variables which we may select from a uniform distribution. For the simulation with $l=d$, we are free to pick $d$ to be any convenient value, so let $d=1$.

import numpy as np

d, l = 1, 1

ntrials = 10000
x = d/2 * np.random.random_sample(ntrials)
theta = np.pi/2 * np.random.random_sample(ntrials)

p = np.sum(x <= l/2 * np.sin(theta)) / ntrials
print('d = {:g}, l = {:g}'.format(d, l))
print('Monte Carlo estimate: {:.5f}, exact answer: {:.5f}'
            .format(p,2*l/np.pi/d))

The output is:

d = 1, l = 1
Monte Carlo estimate: 0.64470, exact answer: 0.63662