Solution P6.4.3
(a) First write the van der Waals constants in SI units and calculate the critical temperature and pressure, $(T_\mathrm{c}, p_\mathrm{c})$:
In [x]: a = 4.225 / 1.e6 * 1.e5 # m^6.Pa.mol^-2
In [x]: b = 0.03707 / 1.e3 # m^3.mol^-1
In [x]: R = 8.314 # J.K^-1.mol^-1
In [x]: Tc, pc = 8*a/27/R/b, a/27/b**2
In [x]: print('Tc = {:.1f} K, pc = {:.1f} MPa'.format(Tc, pc/1.e6))
Tc = 406.2 K, pc = 11.4 MPa
Next define a function returning a Polynomial object representing the equation of state:
In [x]: import numpy as np
In [x]: Polynomial = np.polynomial.Polynomial
In [x]: def get_poly(a, b, T, p):
...: return Polynomial([-a*b, a, -(p*b + R*T), p])
Room temperature (298 K) and pressure ($1\;\mathrm{atm} = 101325\;\mathrm{Pa}$) are below the critical point, and so we expect three roots, from which we want the smallest and largest:
In [x]: poly = get_poly(a, b, 298., 101325.)
In [x]: roots = poly.roots()
In [x]: roots.sort()
In [x]: Vliq, Vgas = roots[0], roots[-1]
In [x]: print('V(liq) = {:.1f} cm^3.mol^-1\n'
'V(gas) = {:.1f} dm^3.mol^-1'.format(Vliq*1.e6, Vgas*1.e3))
V(liq) = 54.4 cm^3.mol^-1
V(gas) = 24.3 dm^3.mol^-1
At $(500\;\mathrm{K}, 12\;\mathrm{MPa})$ we are above the critical point and there is only one real root:
In [x]: poly = get_poly(a, b, 500, 12.e6)
In [x]: roots = poly.roots()
In [x]: Vgas = roots[roots.imag==0][0].real
In [x]: print('V(gas) = {:.1f} cm^3.mol^-1'.format(Vgas*1.e6))
V(gas) = 271.5 cm^3.mol^-1
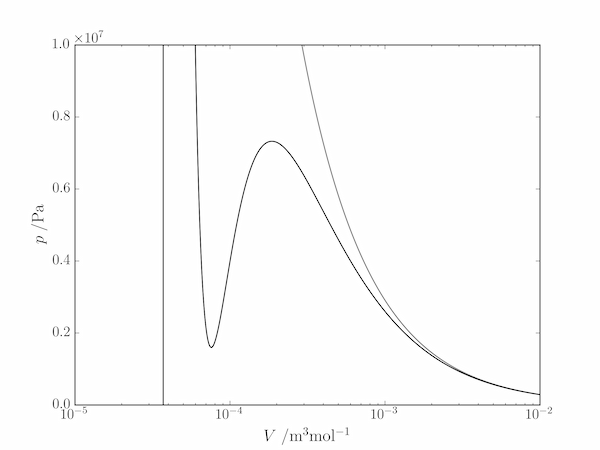
(b) 350 K is below the critical point, so ammonia will condense under sufficient compression. The molar volume will therefore span several orders of magnitude between $10^{-5}$ and $10^{-2}\;\mathrm{m^3}$ and a log scale is appropriate.
In [x]: import matplotlib.pyplot as plt
In [x]: T = 350
In [x]: V = np.logspace(-5,-2,1000)
In [x]: plt.plot(V, R*T/V, color='gray')
In [x]: plt.plot(V, R*T/(V-b) - a*V**-2, 'k')
In [x]: plt.ylim(0, 1.e7)
In [x]: plt.xscale('log')
In [x]: plt.show()