Solution P3.1.1
If you run the code below the output should be something like the graph shown here.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-20, 20, 1000)
def f1(x):
return np.log(np.sin(x)**-2)
def f2(x):
return np.log(np.cos(x)**-2)
plt.plot(x, f1(x))
plt.plot(x, f2(x))
plt.show()
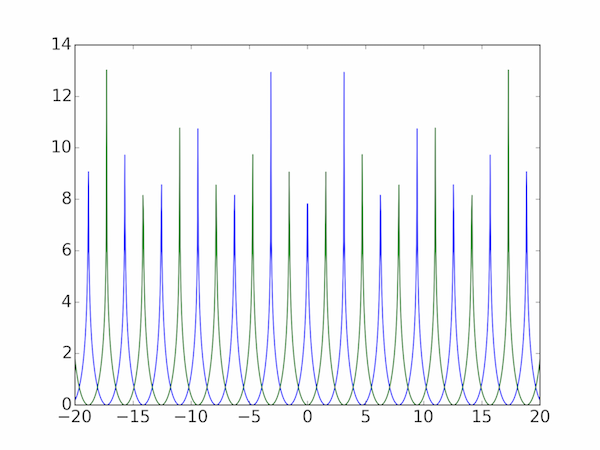
Consider $f_1(x)$. This function is infinite for $x = n\pi$ where $n = 0, 1, 2, \cdots$ as Python will tell you:
>>> f1(0)
__main__:2: RuntimeWarning: divide by zero encountered in double_scalars
inf
However, the discrete grid of $x$ values we have chosen does not actually include any of these points, and so the peaks appear as maxima which vary in height according to how close to $x = n\pi$ the points in x become. For example, in the vicinity of $x=0$:
>>> x[498:502]
array([-0.06006006, -0.02002002, 0.02002002, 0.06006006])
>>> f1(x[498:502])
array([ 5.62602298, 7.82217861, 7.82217861, 5.62602298])
but near $x = \pi$,
>>> x[576:580]
array([ 3.06306306, 3.1031031 , 3.14314314, 3.18318318])
>>> f1(x[576:580])
array([ 5.09061561, 6.51523082, 12.93836992, 6.36034221])