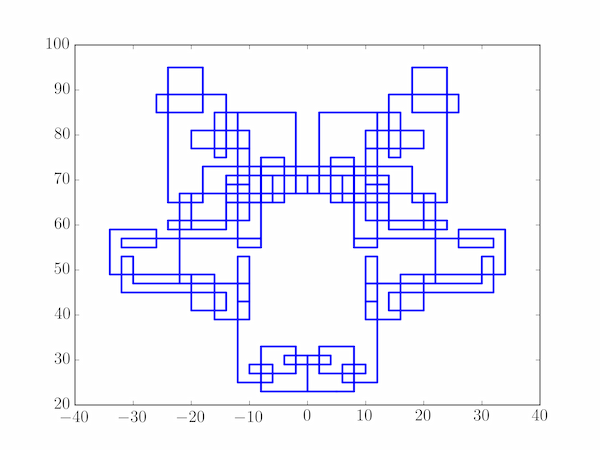
Solution P3.2.2
The following code plots the Gaussian prime spiral starting at $c_0 = 5 + 23i$.
import numpy as np
import matplotlib.pyplot as plt
def is_prime(a):
""" Return True if a is a prime number. """
if a==2:
return True
if not a % 2:
return False
for d in range(3, int(np.sqrt(a)) + 1, 2):
if not a % d:
return False
return True
def is_gaussian_prime(c):
""" Return True if c = x + iy is a Gaussian prime (otherwise False). """
x, y = c
if x==0 or y==0:
a = abs(x) or abs(y)
return is_prime(a) and a % 4 == 3
a = x**2 + y**2
return is_prime(a)
def turn_left(c):
""" Permute (1,0) -> (0,1) -> (-1,0) -> (0,-1) -> (1,0). """
dx, dy = c
return -dy, dx
# Starting point and direction
x, y = x0, y0 = 5, 23
dx, dy = 1, 0
# Keep track of the points on our spiral path in these lists
pathx, pathy = [x], [y]
# It isn't known whether every iteration produces a closed loop so
# set a maximum number of steps to take
max_steps = 10000
step = 0
while step < max_steps:
step += 1
x, y = x+dx, y+dy
pathx.append(x)
pathy.append(y)
if (x,y) == (x0,y0):
print('Returned to ({}, {}) in {} steps.'.format(x, y, step))
break
if is_gaussian_prime((x,y)):
dx, dy = turn_left((dx,dy))
else:
print('max_steps = {} reached.'.format(max_steps))
plt.plot(pathx, pathy, lw=2)
plt.show()