Numerical differentiation

First define a function to return the derivative of $f(x)$ using a provided value for $h$:

In [x]: def calc_deriv(x, f, h):
   ...:     return (f(x+h) - f(x)) / h

and use it to approximate the derivative of $f(x)=e^x$ at $x=1$ for $h$ between $10^{-17}$ and $0.1$ on a logarithmic scale:

In [x]: h = np.logspace(-17,-1,17)
In [x]: derivs = calc_deriv(1, np.exp, h)

We're interested in the differences between these approximations and the true answer, $f'(1) = e$. On a log scale,

In [x]: errors = np.abs(derivs - np.e)
In [x]: pylab.loglog(h, errors, basex=10, basey=10)

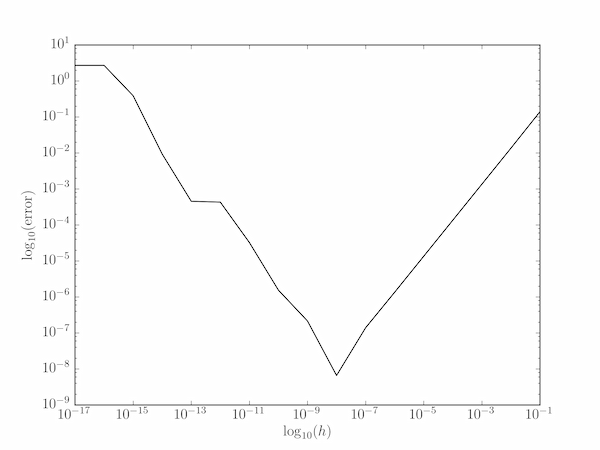
The optimum, $h$, balancing truncation and cancellation errors, is about $10^{-8}$.