Solution P8.2.7
The following code demonstrates the chaotic tumbling behaviour of Hyperion at under some conditions.
import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint
# The orbital eccentricity, e, and (B-A)/C for Hyperion
e, BmAoC = 0.1, 0.265
# Anonymous function for calculating a/r as a function of true anomaly, phi
a_over_r = lambda phi: (1+e*np.cos(phi))/(1-e**2)
def d(z, phi):
"""
Given z = Omega, theta, calculate and return the derivatives,
dOmega/dphi and dtheta/dphi.
"""
Omega, theta = z
aor = a_over_r(phi)
theta_d = aor**-2 * Omega
Omega_d = -BmAoC * 3/2/(1-e**2) * aor * np.sin(2*(theta-phi))
return Omega_d, theta_d
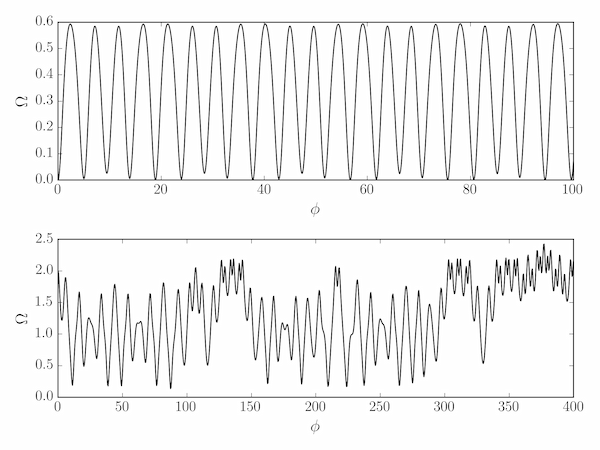
fig = plt.figure()
ax = [fig.add_subplot(rcp) for rcp in (211, 212)]
z0 = [(0,0), (2,0)]
phimax = [100, 400]
for i in range(2):
phi = np.linspace(0, phimax[i], 1000)
Omega, theta = odeint(d, z0[i], phi).T
ax[i].plot(phi, Omega, 'k')
ax[i].set_xlabel(r'$\phi$', fontsize=16)
ax[i].set_ylabel(r'$\Omega$', fontsize=16)
fig.tight_layout()
plt.show()