Solution P8.2.4
We can integrate the two coupled ordinary differential equations with scipy.integrate.odeint() and plot the results in two different ways for the two sets of parameter values, $(a,b)$.
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
fig = plt.figure()
def deriv(X, t, a, b):
x, y = X
dxdt = a - (1+b)*x + x**2 * y
dydt = b*x - x**2 * y
return dxdt, dydt
x0, y0 = 1, 1
t = np.linspace(0, 100, 1000)
def plot_brusselator(a, b, row):
"""
Integrate the Brusselator equations for parameters a,b and plot. """
X = odeint(deriv, (x0, y0), t, args=(a,b))
ax_left = fig.add_subplot(221 + row*2) # Lefthand axis on this row
ax_left.set_color_cycle(['r', 'g'])
ax_left.plot(t, X)
ax_left.legend((r'$x$', r'$y$'), loc='upper right')
ax_left.set_xlabel(r'$t$')
ax_right = fig.add_subplot(222 + row*2) # Righthand axis on this row
ax_right.plot(*X.T, c='b')
ax_right.set_xlabel(r'$x$')
ax_right.set_ylabel(r'$y$')
# Integrate and plot the Brusselator for each of the parameter pairs (1, 1.8)
# and (1, 2.02); the results from each calculation is plotted on a single row
# of the figure identified by row=0 or row=1
plot_brusselator(1, 1.8, 0)
plot_brusselator(1, 2.02, 1)
fig.tight_layout()
plt.show()
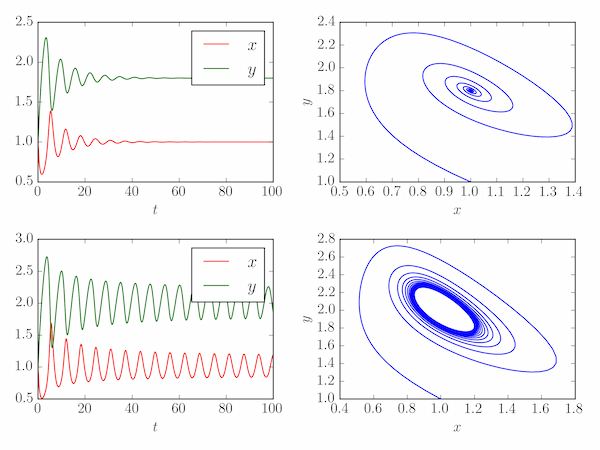
This system displays an Andronov-Hopf bifurcation at $b_\star=a^2 + 1$: for $b$ less this value (top two plots) there is a stable focus: the concentrations of X and Y converge on stable equilibrium values; for $b > b_\star$ the system enters a limit cycle (bottom two plots).