Solution P8.2.2
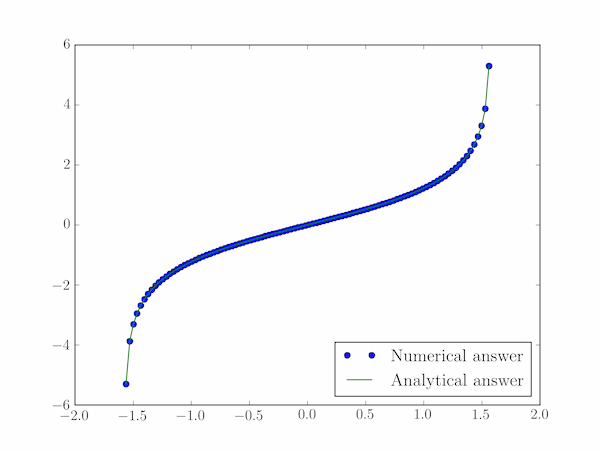
The code below compares the numerical integration of the secant function with the inverse Gudermannian function.
import numpy as np
from scipy.integrate import quad
import pylab
sec = lambda x: 1./np.cos(x)
# evaluate the secant integral for -pi/2 < theta < pi/2
n = 100
theta = np.linspace(-np.pi/2+0.01, np.pi/2-0.01, n)
# Numerical answer by quadrature
I = np.zeros(n)
for i, th in enumerate(theta):
I[i], _ = quad(lambda x: sec(x), 0, th)
# Analytical answer: the inverse Gudermannian function
gdinv = np.log(np.abs(sec(theta) + np.tan(theta)))
pylab.plot(theta, I, 'o', label='Numerical answer')
pylab.plot(theta, gdinv, label='Analytical answer')
pylab.legend(loc=4)
pylab.show()