Question
The NASA Cosmic Background Explorer (COBE) satellite carried an instrument, FIRAS (Far-Infrared Absolute Spectrophotometer) to measure the cosmic microwave background (CMB) radiation, which was confirmed to be distributed according to a black-body curve in accordance with the big bang theory:
\begin{align*} I(\tilde{\nu}, T) = \frac{2h\tilde{\nu}^3c^2}{\exp\left(\frac{hc\tilde{\nu}}{k_\mathrm{B}T}\right) - 1} \end{align*} where the radiation frequency is expressed in wavenumbers, $\mathrm{cm^{-1}}$, and the speed of light, $c$, is taken to be in $\mathrm{cm\,s^{-1}}$.
The data file cmb-data.txt contains measurements of $I(\tilde{\nu})$ based on the FIRAS observations. Note that the units of $I$ in this file are $\mathrm{erg\,s^{-1}\,cm^{-2}\,sr^{-1}\,cm}$ and that $1\;\mathrm{J}\equiv 10^7\;\mathrm{erg}$. Use scipy.optimize.curve_fit to determine the temperature of the CMB and take the estimated $1\sigma$ error in the measurement to be $2 \times 10^{-6}\;\mathrm{erg\,s^{-1}\,cm^{-2}\,sr^{-1}\,cm}$.
Solution
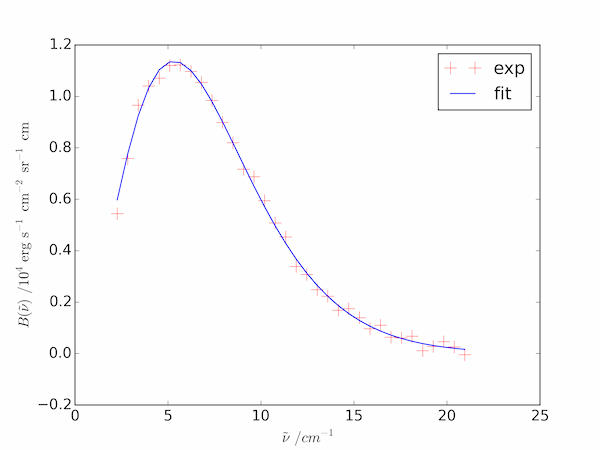
The following code fits the provided CMB data to give a temperature of $2.715 \pm 0.004\;\mathrm{K}$.
# fit_cmb.py
import pylab
import numpy as np
from scipy.constants import h, c, k
c = 100 * c
from scipy.optimize import curve_fit
nu, cmb = np.loadtxt('cmb-data.txt', unpack=True)
def B(nu, T):
return 2 * h * nu**3 * c**2 / (np.exp(h*c*nu/k/T)-1) * 1.e7
sigma = 2.e-6
T0 = 1
popt, pcov = curve_fit(B, nu, cmb, p0=(T0,), sigma=sigma, absolute_sigma=True)
Tfit = popt[0]
Bfit = B(nu, Tfit)
perr = np.sqrt(np.diag(pcov))[0]
print('Tcmb = {:.3f} ± {:.3f} K'.format(Tfit, perr))
pylab.plot(nu, cmb * 1.e4, '+r', markersize=12, label='exp')
pylab.plot(nu, Bfit * 1.e4, label='fit')
pylab.ylabel(r'$B(\tilde{\nu})\,/10^4\mathrm{erg\,s^{-1}\,cm^{-2}\,sr^{-1}\,cm}$')
pylab.xlabel(r'$\tilde{\nu}\,/cm^{-1}$')
pylab.legend()
pylab.show()
Output:
Tcmb = 2.715 ± 0.004 K