Solution P6.1.3
The following solution avoids Python loops by storing the three Gaussian functions in a single array, y, with shape (1000,3).
import numpy as np
import pylab
def gaussian(x, s, m):
return 1./(np.sqrt(2.*np.pi)*s) * np.exp(-0.5*((x-m)/s)**2)
m = 0
s = np.array([0.5, 1, 1.5])
x, dx = np.linspace(-10, 10, 1000, retstep=True)
x = x[:,np.newaxis]
y = gaussian(x,s,m)
# Integrate approximately by direct summation along the x-axis
int_y = np.sum(gaussian(x, s, m), axis=0) * dx
print('If these numbers are 1 (or close to it), then the g(x) is normalized:')
print(int_y)
# Numerical differentiation by the first-order central difference formula
h = 1.e-6
dydx = (gaussian(x+h, s, m) - gaussian(x-h, s, m))/2/h
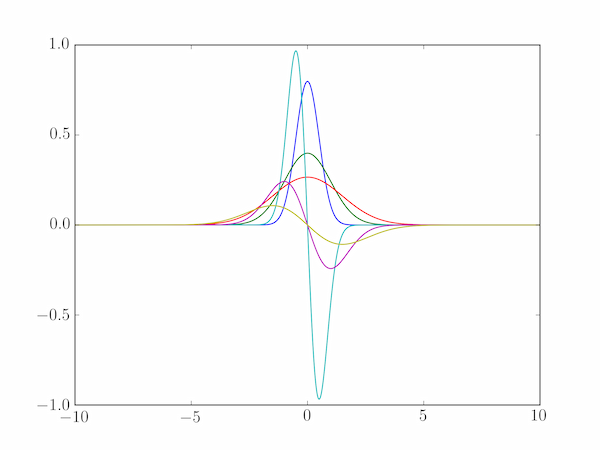
pylab.plot(x, y)
pylab.plot(x, dydx)
pylab.show()