The algorithm
The $k$-means clustering method is a popular algorithm for partitioning a data set into "clusters" in which each data point is assigned to the cluster with the nearest mean. It will be illustrated here with a data set of $n$ points, each of $m=2$ dimensions: $X=[(x_1^{(1)}, x_1^{(2)}), (x_2^{(1)}, x_2^{(2)}), \cdots, (x_n^{(1)}, x_n^{(2)})]$, plotted below.
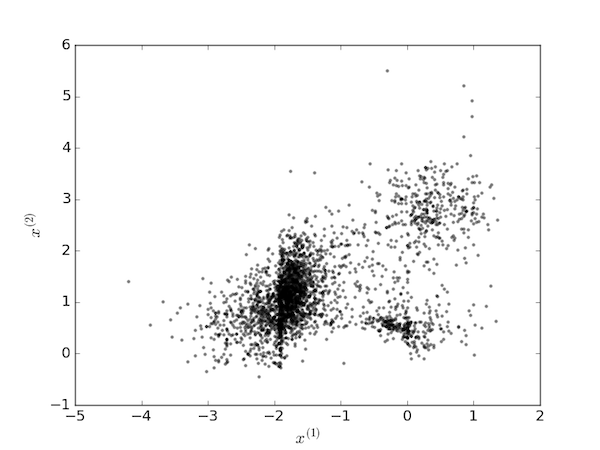
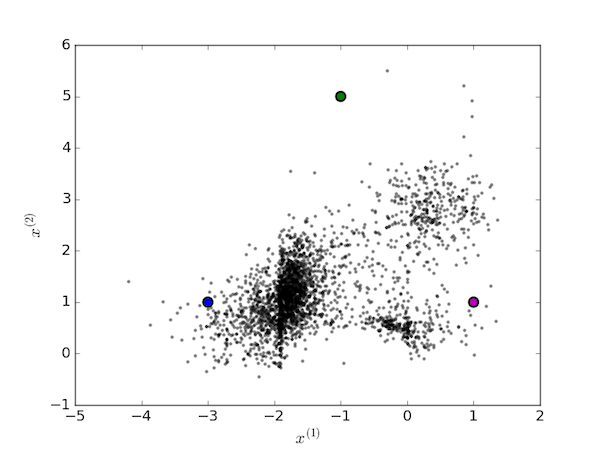
To the human eye, it would seem reasonable to assign these points to $K=3$ clusters. The algorithm proceeds by first picking three random points as the centroids of the clusters:
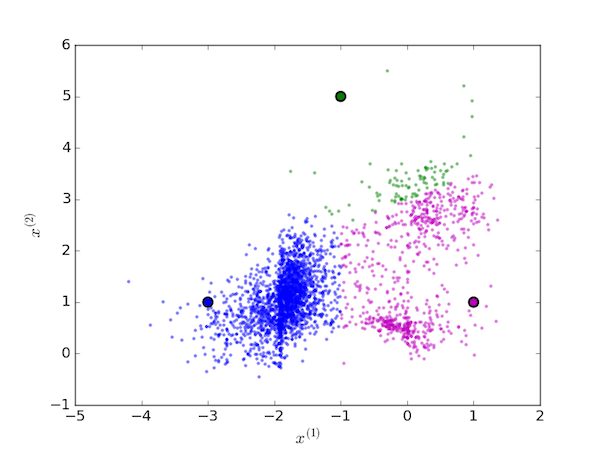
We then iterate over two steps. First assign each data point to the cluster with the nearest centroid:
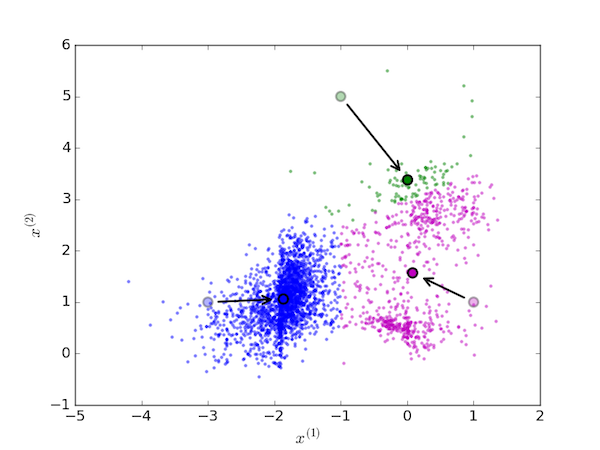
Next, move each centroid to the mean value of the points assigned to it:
On the next iteration, the each data point is again assigned to the cluster with the nearest centroid (since they have moved, this generally means reassigning some of the data points):
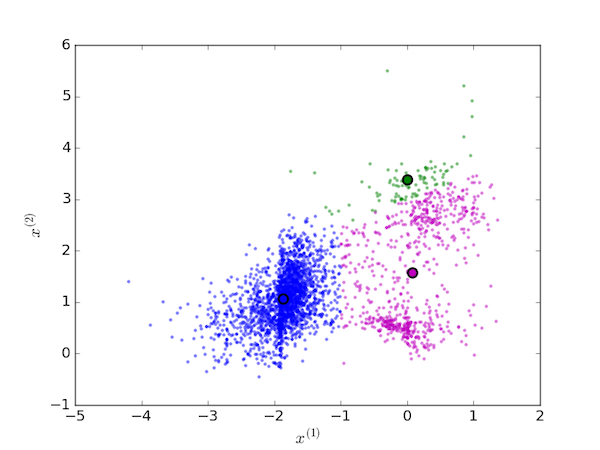
and again, the centroids are moved to the new mean value of each cluster:
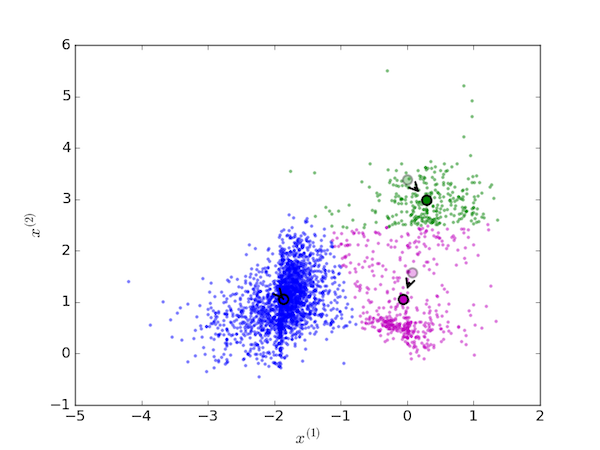
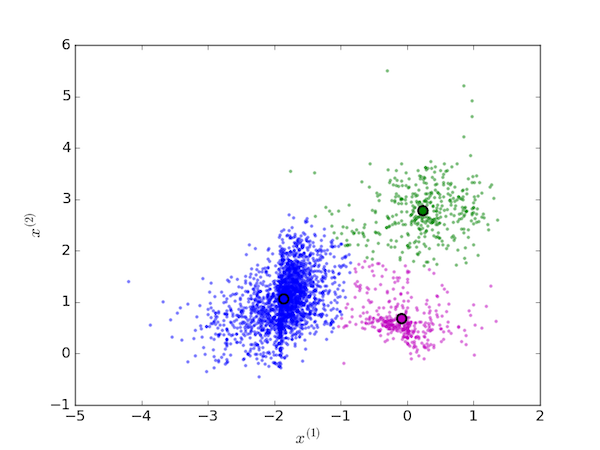
This procedure is replaced until the centroids no longer move because no data points are reassigned. The final cluster assignments for the initial conditions are shown below.
Mathematical details
Mathematically, the $k$-means algorithm partitions the data set into $K$ sets, $\boldsymbol{C} = {C_1, C_2, \cdots, C_K}$, such that the sum of the within-cluster squared distances between each data point and the cluster mean is minimized:
$$ \underset{\boldsymbol{C}}{\arg \min} \sum_{k=1}^K \sum_{\boldsymbol{x} \in C_k} ||\boldsymbol{x} - \boldsymbol{\mu_k}||^2 $$
The $k$-means method is not guaranteed to find the global minimum in this equation and so it is frequently implemented by re-running it several times for different random initial choices for $\boldsymbol{\mu}$ and selecting the clustering with the smallest value of the above summation.
Python implementation
Notes
The cluster assignment step is carried out with this line of code:
k = min([(idx, (x-av) @ (x-av)) for idx, av in enumerate(mu)],
key=lambda e:e[1])[0]
The squared distance between data point $\boldsymbol{x}$ (x) and the mean of cluster $i$, $\boldsymbol{\mu}_i$ (av = mu[idx]) is calculated as the vector dot product, (x-av) @ (x-av) implemented with Python's new @ infix operator. This expression can be replaced with np.dot((x-av), (x-av)) in versions of Python earlier than 3.5. The list comprehension then generates the index into the cluster average array and value of the squared distance between each data point and that cluster average. From this list, the index with the minimum distance is returned and set to k: that is, the index of the cluster with the smallest distance between its mean and the data point.
The cluster means (centroids) are moved in another single line of code:
mu = [np.mean(clusters[k], axis=0) for k in range(len(mu))]
This simply resets the list of vectors mu to the average value of each cluster's data points. The argument axis=0 ensures we average over the observations but not over each dimension of the data vectors.
Warning
This code is an illustration of a vectorized implementation of the $k$-means algorithm only and for study by people learning Python and NumPy. It is not optimized implementation of the algorithm for "production" use: for that, consider using the KMeans class from the scikit-learn Python machine learning package.
The code
The first function defined, kmeans, performs a single run of the $k$-means algorithm and partitions the provided data, X, into nclusters ($K$) clusters. The second function, kmeans_pp runs kmeans a given number of times, nrepeat, and returns the optimum clustering found over these runs.
import numpy as np
def kmeans(X, nclusters):
"""Perform k-means clustering with nclusters clusters on data set X.
Returns mu, an ordered list of the cluster centroids and clusters, a
list of nclusters lists containing the clustered points from X.
X is an array of of shape (n,m) containing n data points (observations)
each of dimension m.
nclusters (also commonly referred to as K) is the number of clusters to
partition the data into.
"""
def assign_clusters(X, mu):
"""Assign points from X to clusters centered on points mu."""
# The clustered points will be put in m independent lists in clusters:
m = len(mu)
clusters = [[] for i in range(m)]
# Assign each data point (observation) to a cluster indexed by k such
# that the squared distance between the observation and that cluster's
# mean is a minimum.
for x in X:
k = min([(idx, (x-av) @ (x-av)) for idx, av in enumerate(mu)],
key=lambda e:e[1])[0]
clusters[k].append(x)
return clusters
def move_centroids(mu, clusters):
"""Move the centroids of each cluster to that cluster's average."""
mu = [np.mean(clusters[k], axis=0) for k in range(len(mu))]
return mu
def is_converged(mu, oldmu):
"""Return True if the centroids mu and oldmu are the same.
If the centroid positions are the same the clustering has converged.
"""
return np.allclose(np.sort(mu, axis=1), np.sort(oldmu, axis=1))
# Pick some random data points as the initial cluster centroids.
mu = X[np.random.choice(X.shape[0], nclusters, replace=False),:]
# Iterate the k-means algorithm to convergence.
while True:
oldmu = mu
clusters = assign_clusters(X, mu)
mu = move_centroids(mu, clusters)
if is_converged(mu, oldmu):
break
return mu, clusters
def kmeans_pp(X, nclusters, nrepeat, verbose=False):
"""Repeat the k-means algoritm nrepeat times, picking the optimum.
X is an array of of shape (n,m) containing n data points (observations)
each of dimension m.
nclusters (also commonly referred to as K) is the number of clusters to
partition the data into.
nrepeat is the number of runs of the k-means algorithm to repeat with
different random initial cluster centroids in order to pick the best one.
verbose = True/False turns on/off some progress reporting.
"""
if verbose:
print('iteration | this goodness | best goodness')
print('-----------------------------------------')
best_goodness = None
for i in range(nrepeat):
mu, clusters = kmeans(X, nclusters)
this_goodness = np.sum([np.sum(np.linalg.norm(cluster-mu[k]))
for k, cluster in enumerate(clusters)])
if best_goodness is None or best_goodness > this_goodness:
best_goodness = this_goodness
best_clustering = mu, clusters
if verbose:
print('{:^9d} | {:13g} | {:13g}'.format(i+1, this_goodness,
best_goodness))
return best_clustering