The following code implements a Quadtree in Python (see the previous blog post for a description of quadtrees). There are three classes: Point represents a point in two-dimensional space, with an optional "payload" (data structure associating the Point with more information, for example the identity of an object). The Rect class represents a rectangle in two-dimensional space through its centre, width and height. There are methods to determine if a given Point object is inside the Rect and to determine if the Rect intersects another Rect.

Finally, the QuadTree class represents the quadtree data structure itself. It is defined recursively, such that when a node needs to divide, it spawns four child Quadtrees within its domain (idenfied as northwest, northeast, southwest, southeast).

import numpy as np

class Point:
    """A point located at (x,y) in 2D space.

    Each Point object may be associated with a payload object.

    """

    def __init__(self, x, y, payload=None):
        self.x, self.y = x, y
        self.payload = payload

    def __repr__(self):
        return '{}: {}'.format(str((self.x, self.y)), repr(self.payload))
    def __str__(self):
        return 'P({:.2f}, {:.2f})'.format(self.x, self.y)

    def distance_to(self, other):
        try:
            other_x, other_y = other.x, other.y
        except AttributeError:
            other_x, other_y = other
        return np.hypot(self.x - other_x, self.y - other_y)

class Rect:
    """A rectangle centred at (cx, cy) with width w and height h."""

    def __init__(self, cx, cy, w, h):
        self.cx, self.cy = cx, cy
        self.w, self.h = w, h
        self.west_edge, self.east_edge = cx - w/2, cx + w/2
        self.north_edge, self.south_edge = cy - h/2, cy + h/2

    def __repr__(self):
        return str((self.west_edge, self.east_edge, self.north_edge,
                self.south_edge))

    def __str__(self):
        return '({:.2f}, {:.2f}, {:.2f}, {:.2f})'.format(self.west_edge,
                    self.north_edge, self.east_edge, self.south_edge)

    def contains(self, point):
        """Is point (a Point object or (x,y) tuple) inside this Rect?"""

        try:
            point_x, point_y = point.x, point.y
        except AttributeError:
            point_x, point_y = point

        return (point_x >= self.west_edge and
                point_x <  self.east_edge and
                point_y >= self.north_edge and
                point_y < self.south_edge)

    def intersects(self, other):
        """Does Rect object other interesect this Rect?"""
        return not (other.west_edge > self.east_edge or
                    other.east_edge < self.west_edge or
                    other.north_edge > self.south_edge or
                    other.south_edge < self.north_edge)

    def draw(self, ax, c='k', lw=1, **kwargs):
        x1, y1 = self.west_edge, self.north_edge
        x2, y2 = self.east_edge, self.south_edge
        ax.plot([x1,x2,x2,x1,x1],[y1,y1,y2,y2,y1], c=c, lw=lw, **kwargs)


class QuadTree:
    """A class implementing a quadtree."""

    def __init__(self, boundary, max_points=4, depth=0):
        """Initialize this node of the quadtree.

        boundary is a Rect object defining the region from which points are
        placed into this node; max_points is the maximum number of points the
        node can hold before it must divide (branch into four more nodes);
        depth keeps track of how deep into the quadtree this node lies.

        """

        self.boundary = boundary
        self.max_points = max_points
        self.points = []
        self.depth = depth
        # A flag to indicate whether this node has divided (branched) or not.
        self.divided = False

    def __str__(self):
        """Return a string representation of this node, suitably formatted."""
        sp = ' ' * self.depth * 2
        s = str(self.boundary) + '\n'
        s += sp + ', '.join(str(point) for point in self.points)
        if not self.divided:
            return s
        return s + '\n' + '\n'.join([
                sp + 'nw: ' + str(self.nw), sp + 'ne: ' + str(self.ne),
                sp + 'se: ' + str(self.se), sp + 'sw: ' + str(self.sw)])

    def divide(self):
        """Divide (branch) this node by spawning four children nodes."""

        cx, cy = self.boundary.cx, self.boundary.cy
        w, h = self.boundary.w / 2, self.boundary.h / 2
        # The boundaries of the four children nodes are "northwest",
        # "northeast", "southeast" and "southwest" quadrants within the
        # boundary of the current node.
        self.nw = QuadTree(Rect(cx - w/2, cy - h/2, w, h),
                                    self.max_points, self.depth + 1)
        self.ne = QuadTree(Rect(cx + w/2, cy - h/2, w, h),
                                    self.max_points, self.depth + 1)
        self.se = QuadTree(Rect(cx + w/2, cy + h/2, w, h),
                                    self.max_points, self.depth + 1)
        self.sw = QuadTree(Rect(cx - w/2, cy + h/2, w, h),
                                    self.max_points, self.depth + 1)
        self.divided = True

    def insert(self, point):
        """Try to insert Point point into this QuadTree."""

        if not self.boundary.contains(point):
            # The point does not lie inside boundary: bail.
            return False
        if len(self.points) < self.max_points:
            # There's room for our point without dividing the QuadTree.
            self.points.append(point)
            return True

        # No room: divide if necessary, then try the sub-quads.
        if not self.divided:
            self.divide()

        return (self.ne.insert(point) or
                self.nw.insert(point) or
                self.se.insert(point) or
                self.sw.insert(point))

    def query(self, boundary, found_points):
        """Find the points in the quadtree that lie within boundary."""

        if not self.boundary.intersects(boundary):
            # If the domain of this node does not intersect the search
            # region, we don't need to look in it for points.
            return False

        # Search this node's points to see if they lie within boundary ...
        for point in self.points:
            if boundary.contains(point):
                found_points.append(point)
        # ... and if this node has children, search them too.
        if self.divided:
            self.nw.query(boundary, found_points)
            self.ne.query(boundary, found_points)
            self.se.query(boundary, found_points)
            self.sw.query(boundary, found_points)
        return found_points


    def query_circle(self, boundary, centre, radius, found_points):
        """Find the points in the quadtree that lie within radius of centre.

        boundary is a Rect object (a square) that bounds the search circle.
        There is no need to call this method directly: use query_radius.

        """

        if not self.boundary.intersects(boundary):
            # If the domain of this node does not intersect the search
            # region, we don't need to look in it for points.
            return False

        # Search this node's points to see if they lie within boundary
        # and also lie within a circle of given radius around the centre point.
        for point in self.points:
            if (boundary.contains(point) and
                    point.distance_to(centre) <= radius):
                found_points.append(point)

        # Recurse the search into this node's children.
        if self.divided:
            self.nw.query_circle(boundary, centre, radius, found_points)
            self.ne.query_circle(boundary, centre, radius, found_points)
            self.se.query_circle(boundary, centre, radius, found_points)
            self.sw.query_circle(boundary, centre, radius, found_points)
        return found_points

    def query_radius(self, centre, radius, found_points):
        """Find the points in the quadtree that lie within radius of centre."""

        # First find the square that bounds the search circle as a Rect object.
        boundary = Rect(*centre, 2*radius, 2*radius)
        return self.query_circle(boundary, centre, radius, found_points)


    def __len__(self):
        """Return the number of points in the quadtree."""

        npoints = len(self.points)
        if self.divided:
            npoints += len(self.nw)+len(self.ne)+len(self.se)+len(self.sw)
        return npoints

    def draw(self, ax):
        """Draw a representation of the quadtree on Matplotlib Axes ax."""

        self.boundary.draw(ax)
        if self.divided:
            self.nw.draw(ax)
            self.ne.draw(ax)
            self.se.draw(ax)
            self.sw.draw(ax)

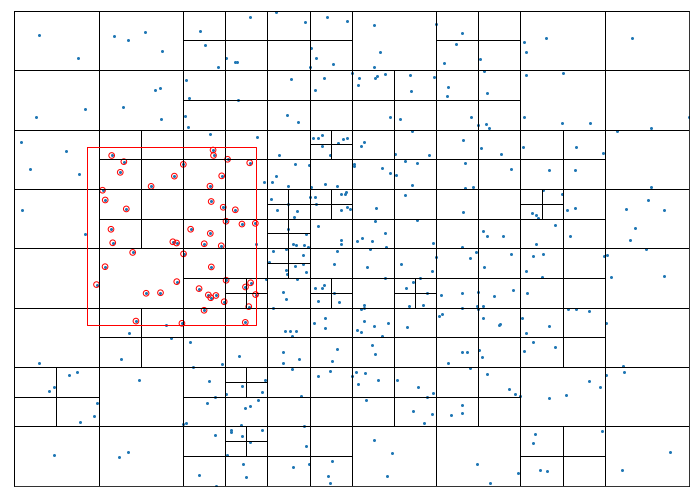
In the following test, the domain is populated with points from a two-dimensional normal distribution. These are stored in a quadtree which is then queried for points that fall within a rectangle defined by Rect(140, 190, 150, 150). This query is efficient in that it onlyt examines nodes whose boundaries intersect with the search area, ignoring those containg only points which lie outside it. The found points are highlighted in red in the figure below.

import numpy as np
import matplotlib.pyplot as plt
from quadtree import Point, Rect, QuadTree
from matplotlib import gridspec

DPI = 72
np.random.seed(60)

width, height = 600, 400

N = 500
coords = np.random.randn(N, 2) * height/3 + (width/2, height/2)
points = [Point(*coord) for coord in coords]

domain = Rect(width/2, height/2, width, height)
qtree = QuadTree(domain, 3)
for point in points:
    qtree.insert(point)

print('Number of points in the domain =', len(qtree))

fig = plt.figure(figsize=(700/DPI, 500/DPI), dpi=DPI)
ax = plt.subplot()
ax.set_xlim(0, width)
ax.set_ylim(0, height)
qtree.draw(ax)

ax.scatter([p.x for p in points], [p.y for p in points], s=4)
ax.set_xticks([])
ax.set_yticks([])

region = Rect(140, 190, 150, 150)
found_points = []
qtree.query(region, found_points)
print('Number of found points =', len(found_points))

ax.scatter([p.x for p in found_points], [p.y for p in found_points],
           facecolors='none', edgecolors='r', s=32)

region.draw(ax, c='r')

ax.invert_yaxis()
plt.tight_layout()
plt.savefig('search-quadtree.png', DPI=72)
plt.show()

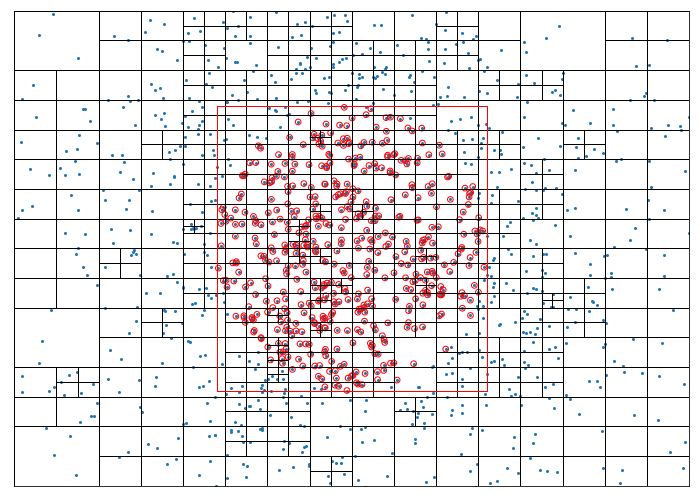
A similar test searches for points a fixed distance (radius) from some provided central point (centre) by constructing the bounding Rect and rejecting points inside it that do not lie within radius or centre.

import numpy as np
import matplotlib.pyplot as plt
from quadtree import Point, Rect, QuadTree
from matplotlib import gridspec

DPI = 72
np.random.seed(60)

width, height = 600, 400

N = 1500
coords = np.random.randn(N, 2) * height/3 + (width/2, height/2)
points = [Point(*coord) for coord in coords]

domain = Rect(width/2, height/2, width, height)
qtree = QuadTree(domain, 3)
for point in points:
    qtree.insert(point)

print('Number of points in the domain =', len(qtree))

fig = plt.figure(figsize=(700/DPI, 500/DPI), dpi=DPI)
ax = plt.subplot()
ax.set_xlim(0, width)
ax.set_ylim(0, height)
qtree.draw(ax)

ax.scatter([p.x for p in points], [p.y for p in points], s=4)
ax.set_xticks([])
ax.set_yticks([])

centre, radius = (width/2, height/2), 120
found_points = []
qtree.query_radius(centre, radius, found_points)
print('Number of found points =', len(found_points))

ax.scatter([p.x for p in found_points], [p.y for p in found_points],
           facecolors='none', edgecolors='r', s=32)

circle = plt.Circle(centre, radius, ec='r')
Rect(*centre, 2*radius, 2*radius).draw(ax, c='r')

ax.invert_yaxis()
plt.tight_layout()
plt.savefig('search-quadtree-circle.png', DPI=72)
plt.show()