Higher Orders of Rainbow
Posted by christian on 01 October 2025
A rainbow forms from light refracted and reflected by the water droplets of a rain shower and can consist of more than one arch. The processes that a ray of light undergoes in forming the primary rainbow are illustrated in the diagram below.
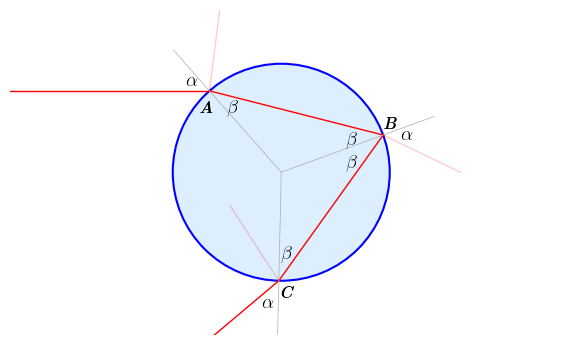
Scattering of a single light ray by a water droplet with one internal reflection.
In the diagram above a light ray encounters the droplet, which is assumed to be spherical, at an angle $\alpha$ to the normal at $A$. It is partly reflected and partly refracted at an angle $\beta$ into the drop, where it hits the internal surface at the back of the droplet at $B$. The majority of the light is then further refracted and leaves the drop, but a small amount is reflected off this back surface where it leaves the droplet at $C$. In being refracted out of the droplet at $C$ it has been turned through a total angle $\phi_1(\alpha) = \alpha - \beta + (\pi - 2\beta) + \alpha - \beta = \pi - 4\beta - \alpha$, where Snell's law relates the angles $\alpha$ and $\beta$:
$$ n_1\sin \alpha = n_2 \sin\beta \quad \Rightarrow \; \sin\alpha = n\sin\beta, $$
since for our purposes, the refractive index of medium 1 (the air) is $n_1 = 1$ and that of water (medium 2) is $n_2 = n \approx 1.33$.
Of course, there are rays arriving from the sun at all points on the front of the droplet. They are almost parallel (though not quite because the sun is not a point source and subtends an angle of about 0.5° to a viewer on Earth). The figure below shows a plot of several such rays: as the incident angle, $\alpha$, varies there is a minimum deflection angle at which they bunch up: the light intensity at this turning point is a maximum and is observed as the (primary) rainbow.
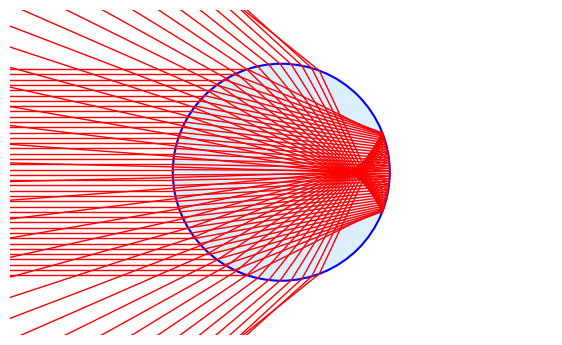
Multiple rays deflected by a single internal reflection in a water droplet.
The deflection angle corresponding to the primary rainbow can be found by differentiating $\phi_1(\alpha)$. First, using Snell's law:
$$ \phi_1 = \pi - 4\beta + 2\alpha = \pi -4\arcsin\left(\frac{1}{n}\sin\alpha\right) + 2\alpha $$
At the stationary point,
$$ \begin{align*} & \frac{\mathrm{d}\psi_1}{\mathrm{d}\alpha} = 2-4\frac{1}{\sqrt{1-\frac{1}{n^2}\sin^2\alpha}} \frac{1}{n}\cos\alpha = 0\\ \Rightarrow & 4\cos^2\alpha = n^2 - \sin^2\alpha\\ \Rightarrow & \cos^2\alpha = \frac{n^2-1}{3} \end{align*} $$
and therefore
$$ \alpha = \arccos\left(\sqrt{\frac{n^2-1}{3}}\right) = \arcsin\left(\sqrt{1-\frac{n^2-1}{3}}\right). $$
For air ($n=1.33$) the incidence angle giving the minimum deflection is therefore $\alpha = 59.6^\circ$, giving a deflection angle of $\phi_1 = 137.5$. The angular height of the rainbow is then $\pi - \phi_1$, about $42.5^\circ$. This angle is called the rainbow angle. The colours of a rainbow result from the fact that $\phi_1$ is slightly different for different wavelengths of light because of the variation of the refractive index of water between red (1.33141) and violet (1.34451) light. The result is that red light is deflected at a relatively steeper viewing angle (42.3°) than violet light (40.4°): the rainbow appears to have an angular width of about 2°.
Notes
- $\beta=40.4^\circ$ is fairly close to Brewster's angle for the air/water interface (about 53°), which accounts for the fact that rainbows are strongly polarized;
- The light reflected at $B$ does not under go total internal reflection, since $\beta$ is less than the critical angle for the air/water interface, $\theta_\mathrm{c} = \arcsin(1/n) = 48.8^\circ$.
- A rainbow can only be seen if the sun is at an angle of less than $42.5^\circ$ in the sky (unless the viewer is above the rain drops, for example in an aeroplane or standing on a mountain looking into a valley).
Secondary Rainbow
A secondary rainbow is often visible outside the primary bow. This is caused by light rays that have undergone two internal reflections in the raindrops:
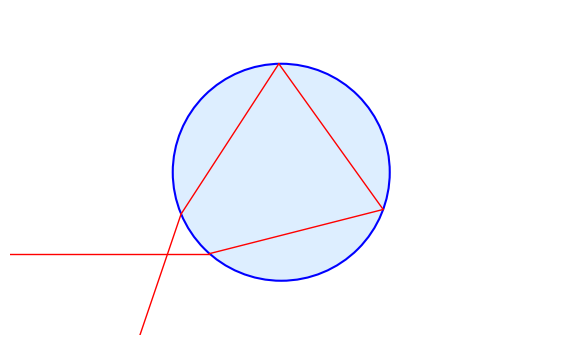
Two internal reflections in a water droplet, which give rise to a secondary rainbow.
The secondary bow appears between 50° and 53° and, because of the second reflection its colours are reversed: the violet arc is on the outside of the bow.
The entry and exit refraction and an arbitrary number of internal reflections, $k$, can be visualized using the code below.
import matplotlib.pyplot as plt
import numpy as np
def plot_ray(n, y0, c='r', x0=-2.5, k=1, ray_lw=1):
"""
Plots the path of a light ray through a spherical droplet,
including one internal reflection. The droplet has unit radius and
is centred on the origin. The ray originates at (x0, y0) and
travels horizontally. n is the refractive index of the material of
the droplet at the wavelength of the light ray.
"""
# 1. Incident Ray (from start at (x0, y0) to point A where it enters the droplet).
chiA = np.pi - np.arcsin(y0)
A = np.exp(1j * chiA) # Point A on the unit circle representing the droplet.
ax.plot([x0, A.real], [y0, A.imag], c=c, lw=ray_lw)
# 2. Refracted Ray (from A to B, inside the droplet).
alpha = np.pi - chiA
# Snells law, n_i.sin(alpha) = n_r.sin(beta) for n_i = 1, n_r = n.
beta = np.arcsin(np.sin(alpha) / n) # Snell's Law
for _ in range(k+1):
# Point on the circle (where the refracted ray hits the inside of the droplet).
chiB = chiA - (np.pi - 2 * beta)
B = np.exp(1j * chiB)
ax.plot([A.real, B.real], [A.imag, B.imag], c=c, lw=ray_lw)
chiA, A = chiB, B
# 4a. Exiting Ray (from B out of the droplet).
# The final direction angle is derived from the total deviation of the ray:
# Total Deviation from alpha (clockwise) is:
theta_D = k*np.pi + 2*alpha - 2*(k+1)*beta
# Create a direction vector and an endpoint to draw the ray
Dhat = np.exp(-1j * theta_D)
ray_length = 3
end_point = B + ray_length * Dhat
ax.plot([B.real, end_point.real], [B.imag, end_point.imag], c=c, lw=ray_lw)
# Starting position of the incoming ray.
x0, y0 = -2.5, 0.85
# Refractive index of water.
n = 1.33
fig, ax = plt.subplots(figsize=(7, 7))
ax.set_aspect('equal', 'box')
# Draw the water droplet.
ax.add_patch(plt.Circle((0, 0), 1, fc="#ddeeff", edgecolor='b', lw=1.5, label='Water Droplet'))
k = 3
plot_ray(n, y0, 'r', x0, k, ray_lw=1)
ax.set_xlim(x0, -x0)
ax.set_ylim(-1.5, 1.5)
plt.axis("off")
plt.show()The deflection angle for $k$ internal reflections is
$$ \phi_k = k\pi + 2\alpha - 2(k+1)\beta = k\pi + 2\alpha - 2(k+1)\arcsin\left( \frac{1}{n}\sin\alpha \right). $$
As before, differentiating with respect to $\alpha$ and finding $\mathrm{d}\phi_k/\mathrm{d}\alpha=0$ yields
$$ \alpha = \arcsin\left(\sqrt{1 - \frac{n^2-1}{k(k+2)}}\right) $$
so the $k$th rainbow is caused by light deflected by angle
$$ \phi_k = k\pi + 2\arcsin\left(\sqrt{1 - \frac{n^2-1}{k(k+2)}}\right) - 2(k+1)\arcsin\left(\sqrt{1 - \frac{n^2-1}{k(k+2)}}\right). $$
Where this angle is less than 90° or greater than 270° the ray is deflected back towards the incoming direction of the ray and a conventional rainbow may be observed. If the deflection angle is between 90° and 270°, the deflection is in the "forward" direction and a full, circular rainbow would result. This is the case for $k=3$, but the light is usually too faint against the glare of the sun for it to be observed.
The code below produces images of the rainbows predicted up to different orders (without quantitatively adjusting for the brightness of each order). The files colour_system.py and cie-cmf.txt from this blog post on converting a spectrum to a colour are required.
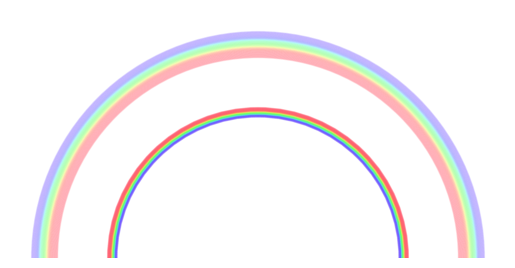
Primary and secondary rainbows.
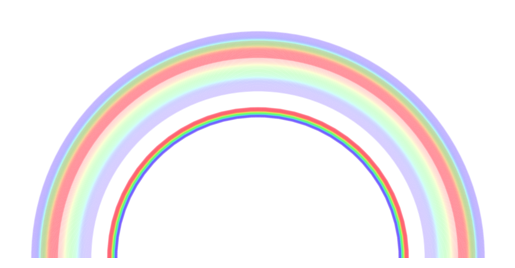
Primary, secondary and fifth-order rainbows. The fifth order bow overlaps the second and is usually too faint to see.
import numpy as np
import matplotlib.pyplot as plt
from colour_system import cs_hdtv
# Draw rainbows of these orders.
RAINBOW_ORDERS = [1, 2, 5]
# Set this flag to True to draw rainbows in the direction away from the sun
# (e.g. primary, secondary rainbows) or False to draw them in the direction
# towards the sun (e.g. tertiary rainbows).
AWAY_FROM_SUN = True
# Draw each ring with this opacity: this has the effect of making higher order
# rainbows look fainter because their colour arcs are more spread out and
# overlap less.
OPACITY = 0.1
# Distance from the viewer to the sheet of rain droplets (in, say, m).
R = 1000
def calc_rainbow_turning_angle(n, k=1):
"""
Calculate the angle through which an incident ray is turned by k internal
reflections in a medium with refractive index n.
"""
fac = np.sqrt(1 - (n**2 - 1) / k / (k + 2))
return k * np.pi - 2 * (k + 1) * np.arcsin(fac / n) + 2 * np.arcsin(fac)
def calc_rainbow_cone_angle(n, k=1, radians=True):
"""
Calculate the cone angle for a rainbow of order k due to scattering by
droplets of refractive index n.
Returns the tuple (away_from_sun, cone_angle) where away_from_sun is a
Boolean flag indicating whether the bow appears in the sky looking away
from the sun (True) or towards the sun (False).
"""
phi_rad = calc_rainbow_turning_angle(n, k)
phi_deg = np.rad2deg(phi_rad) % 360
away_from_sun = False
if 90 < phi_deg < 270:
away_from_sun = True
if phi_deg < 180:
cone_angle = 180 - phi_deg
else:
cone_angle = phi_deg - 180
else:
if phi_deg >= 270:
cone_angle = 360 - phi_deg
else:
cone_angle = phi_deg
if radians:
return away_from_sun, np.deg2rad(cone_angle)
return away_from_sun, cone_angle
# Which rainbows appear away from the sun and which towards the sun?
away_from_sun = {}
for k in range(1, 13):
away_from_sun_flag, cone_angle = calc_rainbow_cone_angle(1.33, k, False)
away_from_sun[k] = away_from_sun_flag
fig, ax = plt.subplots()
ax.set_aspect("equal")
xmax = R * 1.5
ax.set_xlim(-xmax, xmax)
ymin = 0 if AWAY_FROM_SUN else -R * 1.5
ax.set_ylim(ymin, xmax)
plt.axis("off")
cs = cs_hdtv
# The colour system spec is 380 – 780 nm in 5 nm steps but we only need 400 – 700 nm.
Ncslam = 81
colours = []
for i in range(61):
spec = np.zeros(Ncslam)
spec[i + 4] = 1
colours.append(cs.spec_to_rgb(spec, out_fmt="html"))
# Wavelengths (nm) and corresponding refractive indices of water.
lam_red, n_red = 700, 1.33141
lam_violet, n_violet = 400, 1.34451
# Wavelength step of the spectrum grid (nm)
dlam = 5
def add_rainbow_ring(ax, lam, k, c):
n = (lam - lam_red) / (lam_violet - lam_red) * (n_violet - n_red) + n_red
_, rainbow_cone_angle = calc_rainbow_cone_angle(n, k)
z = R * np.tan(rainbow_cone_angle)
c = c[1:]
c = [int(c[i : i + 2], base=16) / 255 for i in range(0, 6, 2)] + [OPACITY]
ax.add_patch(plt.Circle((0, 0), z, fill=False, ec=c))
# Loop over the colours (i.e. wavelengths).
for i in range(61):
spec = np.zeros(Ncslam)
spec[i + 4] = 1
c = cs.spec_to_rgb(spec, out_fmt="html")
lam = lam_violet + i * dlam
# Loop over the rainbow orders, drawing a ring for each.
for k in RAINBOW_ORDERS:
if away_from_sun[k] == AWAY_FROM_SUN:
add_rainbow_ring(ax, lam, k, c)
if not AWAY_FROM_SUN:
# If looking towards the sun, draw a little sun.
ax.add_patch(plt.Circle((0, 0), 50, fc="#ffff00", ec="none"))
plt.show()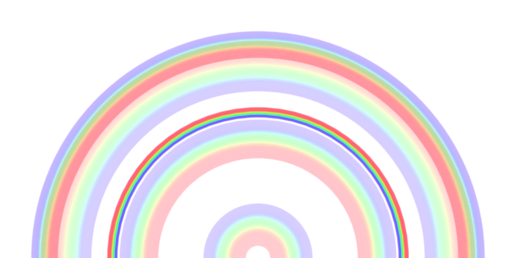
All rainbow orders up to 12 looking away from the sun.