This article presents a Python script to map a spectrum of wavelengths to a representation of a colour. There is no unique way to do this, but the formulation used here is based on the CIE colour matching functions, $\bar{x}(\lambda)$, $\bar{y}(\lambda)$ and $\bar{z}(\lambda)$. These model the chromatic response of a "standard observer" by mapping a power spectrum of wavelengths, $P(\lambda)$, to a set of tristimulus values, $X$, $Y$ and $Z$, analogous to the actual response of the three types of cone cell in the human eye.

$$ \begin{align*} X &= \int P(\lambda)\bar{x}(\lambda)\mathrm{d}\lambda,\\ Y &= \int P(\lambda)\bar{y}(\lambda)\mathrm{d}\lambda,\\ Z &= \int P(\lambda)\bar{z}(\lambda)\mathrm{d}\lambda, \end{align*} $$

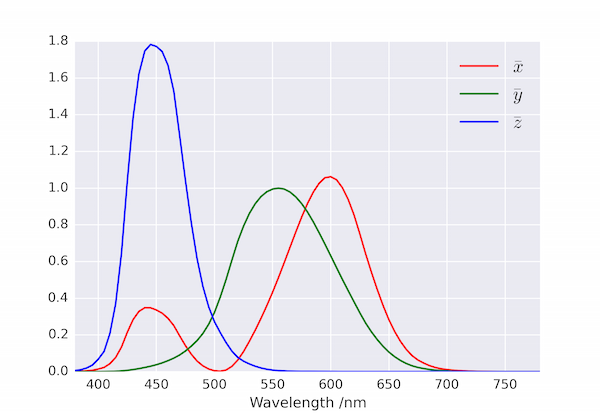
$X$, $Y$ and $Z$ can be normalized by dividing by their sum (at the expense of losing information about the brightness of the light):

$$ x = \frac{X}{X+Y+Z}, \quad y = \frac{Y}{X+Y+Z}, \quad z = \frac{Z}{X+Y+Z} = 1 - x - y $$

In this way, only two parameters, $x$ and $y$ are needed to describe the colour (more accurately, the chromaticity) of the light. The CIE standard chromaticity diagram is shown below.

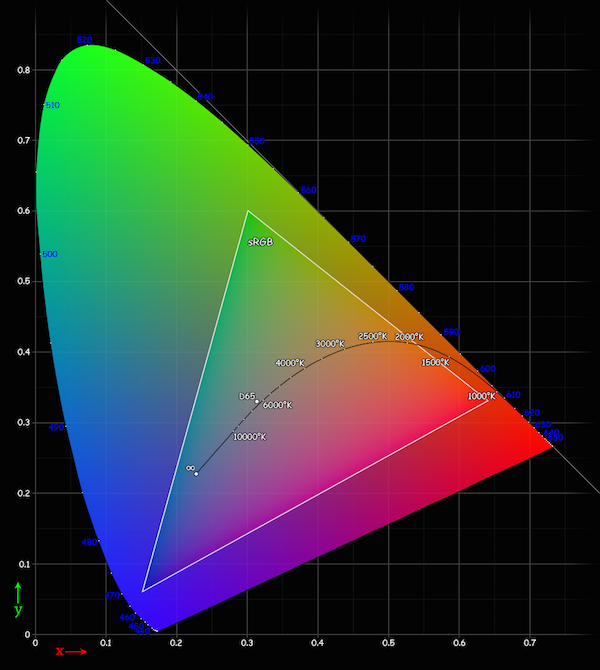
Further conversion of $(x, y)$ to RGB values for output by a display device requires transformation by the appropriate chromaticity matrix. Geometrically, this maps points in the above colour "tongue" onto the subset of points within the RGB "gamut", the indicated triangular region. A colour system may be defined by a matrix of three primary colour chromaticities (the vertices of the triangle) and a white point: a set of chromaticiy coordinates defining the "colour" white for some purpose.

$$ \left( \begin{array}{lll} x_r & x_g & x_b \\ y_r & y_g & y_b \\ z_r & z_g & z_b \end{array} \right) \left( \begin{array}{l} r \\ g \\ b \\ \end{array} \right) = \left( \begin{array}{l} x \\ y \\ z \\ \end{array} \right). $$

Multiplication of the vector of $(x,y,z)$ values by the inverse of this matrix therefore gives the RGB values describing the corresponding colour within the system being used.

Not all $(x, y)$ pairs map to points within the RGB gamut (they would give negative values for one or more component): one way to deal with this is to "desaturate" by raising the values of all components equally until they are all non-negative.

The code below defines a class, ColourSystem, for representing and using colour systems, and instantiates a few particular examples. The CIE matching function is read in from the file cie-cmf.txt.

# colour_system.py
import numpy as np

def xyz_from_xy(x, y):
    """Return the vector (x, y, 1-x-y)."""
    return np.array((x, y, 1-x-y))

class ColourSystem:
    """A class representing a colour system.

    A colour system defined by the CIE x, y and z=1-x-y coordinates of
    its three primary illuminants and its "white point".

    TODO: Implement gamma correction

    """

    # The CIE colour matching function for 380 - 780 nm in 5 nm intervals
    cmf = np.loadtxt('cie-cmf.txt', usecols=(1,2,3))

    def __init__(self, red, green, blue, white):
        """Initialise the ColourSystem object.

        Pass vectors (ie NumPy arrays of shape (3,)) for each of the
        red, green, blue  chromaticities and the white illuminant
        defining the colour system.

        """

        # Chromaticities
        self.red, self.green, self.blue = red, green, blue
        self.white = white
        # The chromaticity matrix (rgb -> xyz) and its inverse
        self.M = np.vstack((self.red, self.green, self.blue)).T 
        self.MI = np.linalg.inv(self.M)
        # White scaling array
        self.wscale = self.MI.dot(self.white)
        # xyz -> rgb transformation matrix
        self.T = self.MI / self.wscale[:, np.newaxis]

    def xyz_to_rgb(self, xyz, out_fmt=None):
        """Transform from xyz to rgb representation of colour.

        The output rgb components are normalized on their maximum
        value. If xyz is out the rgb gamut, it is desaturated until it
        comes into gamut.

        By default, fractional rgb components are returned; if
        out_fmt='html', the HTML hex string '#rrggbb' is returned.

        """

        rgb = self.T.dot(xyz)
        if np.any(rgb < 0):
            # We're not in the RGB gamut: approximate by desaturating
            w = - np.min(rgb)
            rgb += w
        if not np.all(rgb==0):
            # Normalize the rgb vector
            rgb /= np.max(rgb)

        if out_fmt == 'html':
            return self.rgb_to_hex(rgb)
        return rgb

    def rgb_to_hex(self, rgb):
        """Convert from fractional rgb values to HTML-style hex string."""

        hex_rgb = (255 * rgb).astype(int)
        return '#{:02x}{:02x}{:02x}'.format(*hex_rgb)

    def spec_to_xyz(self, spec):
        """Convert a spectrum to an xyz point.

        The spectrum must be on the same grid of points as the colour-matching
        function, self.cmf: 380-780 nm in 5 nm steps.

        """

        XYZ = np.sum(spec[:, np.newaxis] * self.cmf, axis=0)
        den = np.sum(XYZ)
        if den == 0.:
            return XYZ
        return XYZ / den

    def spec_to_rgb(self, spec, out_fmt=None):
        """Convert a spectrum to an rgb value."""

        xyz = self.spec_to_xyz(spec)
        return self.xyz_to_rgb(xyz, out_fmt)

illuminant_D65 = xyz_from_xy(0.3127, 0.3291)
cs_hdtv = ColourSystem(red=xyz_from_xy(0.67, 0.33),
                       green=xyz_from_xy(0.21, 0.71),
                       blue=xyz_from_xy(0.15, 0.06),
                       white=illuminant_D65)

cs_smpte = ColourSystem(red=xyz_from_xy(0.63, 0.34),
                        green=xyz_from_xy(0.31, 0.595),
                        blue=xyz_from_xy(0.155, 0.070),
                        white=illuminant_D65)

cs_srgb = ColourSystem(red=xyz_from_xy(0.64, 0.33),
                       green=xyz_from_xy(0.30, 0.60),
                       blue=xyz_from_xy(0.15, 0.06),
                       white=illuminant_D65)

Here's one application of the ColourSystem class: to visualize the colour of a black body at a given temperature, and example given on this excellent page on the colour rendering of spectra. The spectral radiance of a black body is given by the Planck function:

$$ B(\lambda; T) = \frac{2hc^2}{\lambda^5}\frac{1}{\exp\left(\frac{hc}{\lambda k_\mathrm{B}T}\right) - 1} $$

Feeding $B(\lambda; T)$ as spec to the function ColourSystem.spec_to_rgb returns the RGB components corresponding to the colour of a black body at temperature $T$. This is visualized for different temperatures below.

import numpy as np
from scipy.constants import h, c, k
import matplotlib.pyplot as plt
from matplotlib.patches import Circle

from colour_system import cs_hdtv
cs = cs_hdtv

def planck(lam, T):
    """ Returns the spectral radiance of a black body at temperature T.

    Returns the spectral radiance, B(lam, T), in W.sr-1.m-2 of a black body
    at temperature T (in K) at a wavelength lam (in nm), using Planck's law.

    """

    lam_m = lam / 1.e9
    fac = h*c/lam_m/k/T
    B = 2*h*c**2/lam_m**5 / (np.exp(fac) - 1)
    return B

fig, ax = plt.subplots()

# The grid of visible wavelengths corresponding to the grid of colour-matching
# functions used by the ColourSystem instance.
lam = np.arange(380., 781., 5)

for i in range(24):
    # T = 500 to 12000 K
    T = 500*i + 500

    # Calculate the black body spectrum and the HTML hex RGB colour string
    # it looks like
    spec = planck(lam, T)
    html_rgb = cs.spec_to_rgb(spec, out_fmt='html')

    # Place and label a circle with the colour of a black body at temperature T
    x, y = i % 6, -(i // 6)
    circle = Circle(xy=(x, y*1.2), radius=0.4, fc=html_rgb)
    ax.add_patch(circle)
    ax.annotate('{:4d} K'.format(T), xy=(x, y*1.2-0.5), va='center',
                ha='center', color=html_rgb)

# Set the limits and background colour; remove the ticks
ax.set_xlim(-0.5,5.5)
ax.set_ylim(-4.35, 0.5)
ax.set_xticks([])
ax.set_yticks([])
ax.set_facecolor('k')
# Make sure our circles are circular!
ax.set_aspect("equal")
plt.show()