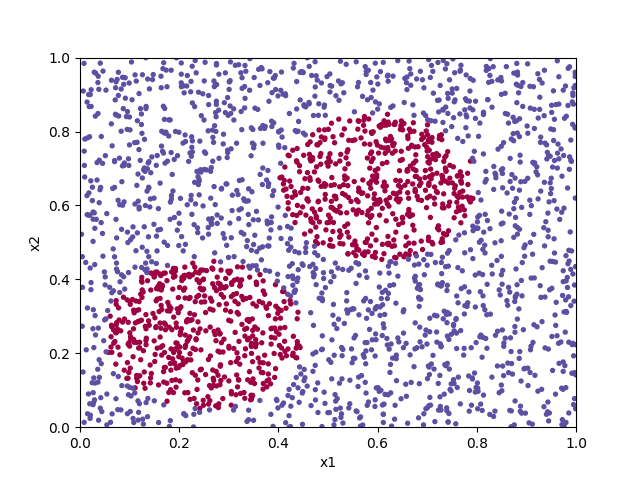
Classification problems are a broad class of machine learning applications devoted to assigning input data to a predefined category based on its features. If the boundary between the categories has a linear relationship to the input data, a simple logistic regression algorithm may do a good job. For more complex groupings, such as in classifying the points in the diagram below, a neural network can often give good results.
In a shallow neural network, the values of the feature vector of the data to be classified (the input layer) are passed to a layer of nodes (also known as neurons or units) (the hidden layer) each of which generates a response according to some activation function, \(g\), acting on the weighted sum of those values, \(z\). The responses of each unit in the hidden layer is then passed to a final, output layer (which may consist of a single unit), whose activation produces the classification prediction output.
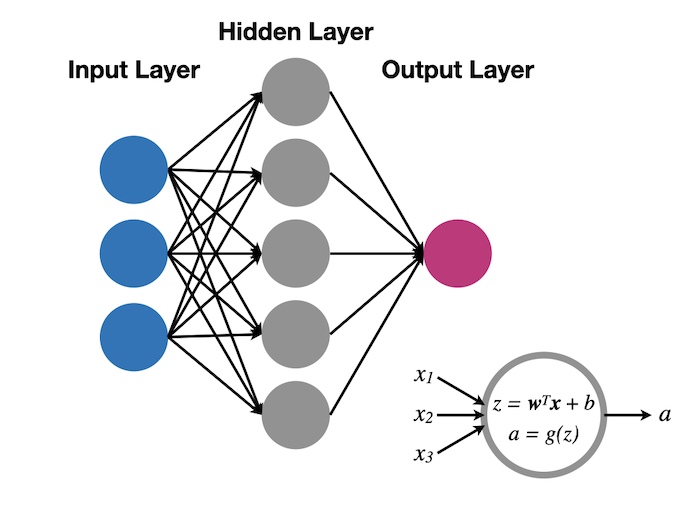
Identifying the layers with superscript labels \([0]\) (input layer), \([1]\) (hidden layer) and \([2]\) (output layer) so that \(a^{[0]}_j \equiv x_j\) are the input feature values, and \(a^{[2]} \equiv \hat{y}\) is the output classification we can write:
Here, \(n^{[\ell]}\) is the number of units in the \(\ell\)th layer; we will consider a binary classification case for which \(n^{[2]} = 1\).
To train the neural network, it is presented with \(m\) training examples, \(\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \ldots, \boldsymbol{x}^{(m)}\) corresponding to known classifications \(y^{(1)}, y^{(2)}, \ldots, y^{(m)}\) and the difference between \(\hat{y}\) and \(y\) (expressed in terms of some cost function) is minimized with respect to the parameters \(w_{jk}^{[\ell]}\) and \(b_j^{[\ell]}\) (\(\ell=1,2\)) as with regular logistic regression.
The \(m\) column input feature vectors can be packed into a \(m \times n^{[0]}\) matrix, \(\boldsymbol{X}\equiv \boldsymbol{A}^{[0]}\), their classifications into a \(1 \times m\) row vector, \(\boldsymbol{Y}\), the unit weights into \(n^{[\ell]} \times n^{[\ell-1]}\) matrices, \(\boldsymbol{W}^{[\ell]}\) (for \(\ell=1,2\)) and the bias constants expressed as \(n^{[\ell]}\times 1\) column vectors, \(\boldsymbol{b}^{[\ell]}\). This allows the above equations to be implemented in matrix algebra as:
There are many nonlinear response functions to choose for \(g^{[\ell]}\), including the logistic function, \(\sigma(z) = (1+\mathrm{e}^{-z})^{-1}\), the closely-related hyperbolic tangent function, \(\mathrm{tanh}\), and the rectified linear unit (ReLU) function, \(x^+ = \mathrm{max}(0,x)\).
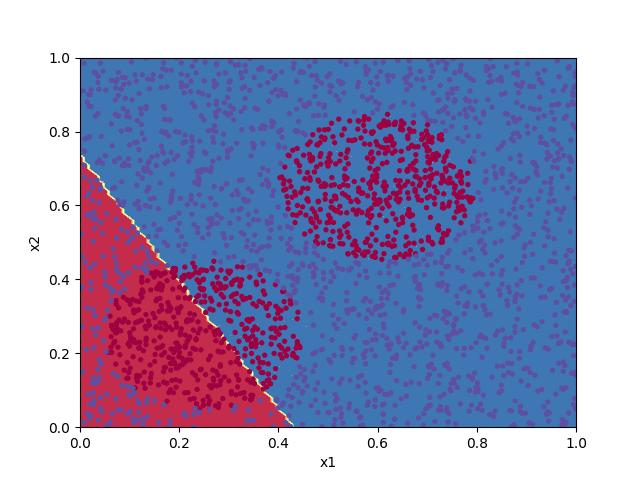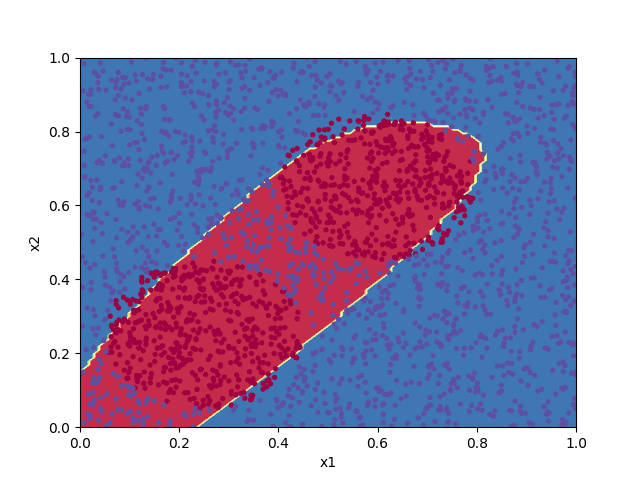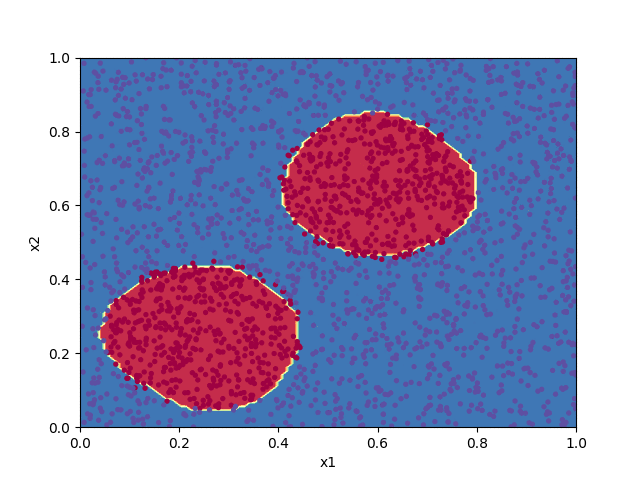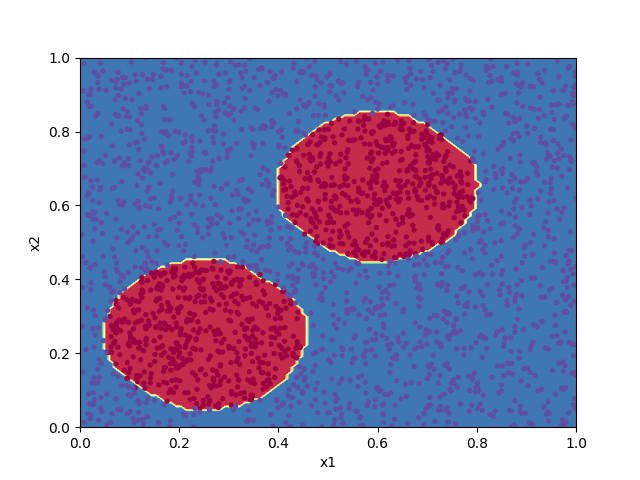
The code below implements a shallow neural network to classify the points in the file pts.txt. Progress in training the algorithm is animated by plotting the decision boundary for the set of parameters \(\boldsymbol{W}^{[\ell]}\) and \(\boldsymbol{b}^{[\ell]}\) at each 100th iteration of the cost function minimization.
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.linear_model
# Training rate.
alpha = 2
# Load the points and ensure shapes are X: (2, m) and Y: (1, m).
pts = np.loadtxt('pts.txt')
X, Y = pts[:,:2].T, pts[:,2][None, :]
# Number of feature vector components (should be 2!).
n0 = X.shape[0]
# Number of training examples.
m = X.shape[1]
# Number of hidden layer units.
n1 = 16
# Number of output units.
n2 = 1
# Activation function for the hidden layer: hyperbolic tan.
g1 = np.tanh
# Activation function for the output layer: logistic function.
def g2(Z):
return 1 / (1 + np.exp(-Z))
def predictions(X, W1, b1, W2, b2):
"""
Return the predictions, A2 (and various intermediate quantities for
caching) for the parameters W1, b1, W2, b2 on the input matrix, X.
"""
Z1 = W1 @ X + b1
A1 = g1(Z1)
Z2 = W2 @ A1 + b2
A2 = g2(Z2)
return Z1, A1, Z2, A2
def cost(Yhat, Y):
"""Evaluate and return the cost function J(Yhat, Y)."""
return -np.sum(Y * np.log(Yhat) + (1 - Y) * np.log(1 - Yhat)) / m
def backprop(A1, Z1, A2, Z2, W1, b1, W2, b2):
"""Backpropagation to update the fit parameters."""
# The derivatives of the cost function with respect to the various
# quantities, dJ/dQ are assigned to variables named dQ.
# For g2 = sigmoid logistic function.
dZ2 = A2 - Y
dW2 = dZ2 @ A1.T / m
db2 = np.sum(dZ2, axis=1, keepdims=True) / m
# For g1 = tanh activation function.
dZ1 = W2.T @ dZ2 * (1 - A1**2)
dW1 = dZ1 @ X.T / m
db1 = np.sum(dZ1, axis=1, keepdims=True) / m
W1 -= alpha * dW1
b1 -= alpha * db1
W2 -= alpha * dW2
b2 -= alpha * db2
return W1, b1, W2, b2
def initialize_params():
"""Randomly initialize the W coefficients, initialize the biases to zero."""
W1 = np.random.randn(n1, n0) * 0.01
b1 = np.zeros((n1, 1))
W2 = np.random.randn(n2, n1) * 0.01
b2 = np.zeros((n2, 1))
return W1, b1, W2, b2
def plot_decision_boundary(X, y, params):
"""Plot the decision boundary for prediction trained on X, y."""
# Set min and max values and give it some padding.
x_min, x_max = X[0, :].min() - 0.1, X[0, :].max() + 0.1
y_min, y_max = X[1, :].min() - 0.1, X[1, :].max() + 0.1
h = 0.01
# Generate a meshgrid of points with orthogonal spacing.
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Prediction of the classified values across the whole grid.
Z = np.round(predictions(np.c_[xx.ravel(), yy.ravel()].T, *params)[-1])
Z = Z.reshape(xx.shape)
# Plot the decision boundary as a contour plot and training examples.
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral, s=8)
plt.ylabel('x2')
plt.xlabel('x1')
def train(X, Y, max_it=1000):
"""Train the neural network on the features X classified as Y."""
W1, b1, W2, b2 = initialize_params()
for it in range(max_it):
Z1, A1, Z2, A2 = predictions(X, W1, b1, W2, b2)
J = cost(A2, Y)
W1, b1, W2, b2 = backprop(A1, Z1, A2, Z2, W1, b1, W2, b2)
if not it % 100:
# Provide an update on the progress we have made so far.
print('{}: J = {}'.format(it, J))
# Clear the current figure and redraw with the latest prediction.
plt.clf()
plot_decision_boundary(X, Y, (W1, b1, W2, b2))
plt.xlim(0,1)
plt.ylim(0,1)
plt.savefig('frames/{:05d}.png'.format(it))
return W1, b1, W2, b2
W1, b1, W2, b2 = train(X, Y, 7000)
plot_decision_boundary(X, Y, (W1, b1, W2, b2))
plt.xlim(0,1)
plt.ylim(0,1)
plt.show()
The frames of the animation are saved as PNG image files to the directory frames/ and can be turned into an animated GIF with, e.g. ImageMagick's convert utility.