Learning Scientific Programming with Python (2nd edition)
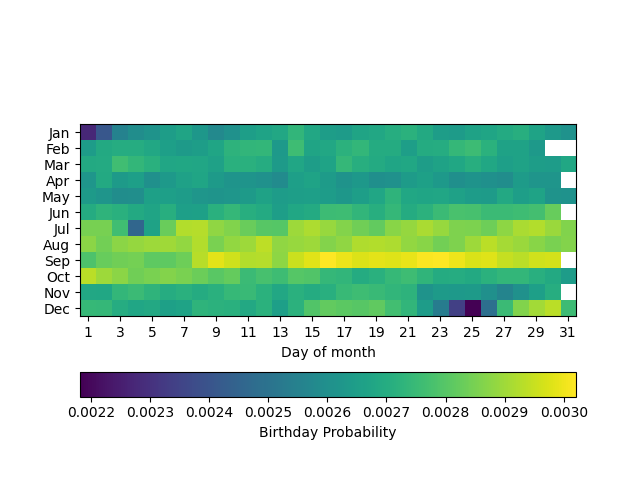
Q7.5.2: A heatmap of birthday dates
Question Q7.5.2
The data provided in the comma-separated file birthday-data.csv gives the number births recorded by the US Centers for Disease Control and Prevention's National Center for Health Statistics for each day of the year as a total from years 1969-1988. The columns are: month number (1=January, 12=December), day number, and number of live births.
Use NumPy to estimate, for each day of the year, the probability of someone's birthday being on that day. Plot the probabilities as a heatmap like that of Example E7.23 and investigate any features of interest.
Hint: the data need "cleaning" to a small extent – inspect the data file first to establish the presence of any incorrect entries.