Learning Scientific Programming with Python (2nd edition)
E7.22: The Barnsley fern
The Barnsley Fern is a fractal which resembles the Black Spleenwort species of fern. It is constructed by plotting a sequence of points in the $(x,y)$ plane, starting at $(0,0)$, generated by the following affine transformations $f_1$, $f_2$, $f_3$, and $f_4$ where each transformation is applied to the previous point and chosen at random with probabilities $p_1 = 0.01$, $p_2 = 0.85$, $p_3 = 0.07$ and $p_4=0.07$. $$ \begin{align*} f_1(x,y) &= \begin{pmatrix} 0 & 0\\0 & 0.16 \end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix}\\[3ex] f_2(x,y) &= \begin{pmatrix} 0.85 & 0.04\\-0.04 & 0.85 \end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} + \begin{pmatrix}0\\1.6\end{pmatrix}\\[3ex] f_3(x,y) &= \begin{pmatrix} 0.2 & -0.26\\0.23 & 0.22 \end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} + \begin{pmatrix}0\\1.6\end{pmatrix}\\[3ex] f_4(x,y) &= \begin{pmatrix} -0.15 & 0.28\\0.26 & 0.24 \end{pmatrix} \begin{pmatrix}x\\y\end{pmatrix} + \begin{pmatrix}0\\0.44\end{pmatrix} \end{align*} $$
This algorithm is implemented in the program below.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
f1 = lambda x, y: (0.0, 0.16 * y)
f2 = lambda x, y: (0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6)
f3 = lambda x, y: (0.2 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6)
f4 = lambda x, y: (-0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44)
fs = [f1, f2, f3, f4]
npts = 50000
# Canvas size (pixels)
width, height = 300, 300
aimg = np.zeros((width, height))
x, y = 0, 0
for i in range(npts):
# Pick a random transformation and apply it
f = np.random.choice(fs, p=[0.01, 0.85, 0.07, 0.07])
x, y = f(x, y)
# Map (x,y) to pixel coordinates.
# NB we "know" that -2.2 < x < 2.7 and 0 <= y < 10
ix, iy = int(width / 2 + x * width / 10), int(y * height / 12)
# Set this point of the array to 1 to mark a point in the fern
aimg[iy, ix] = 1
plt.imshow(aimg[::-1, :], cmap=cm.Greens)
plt.show()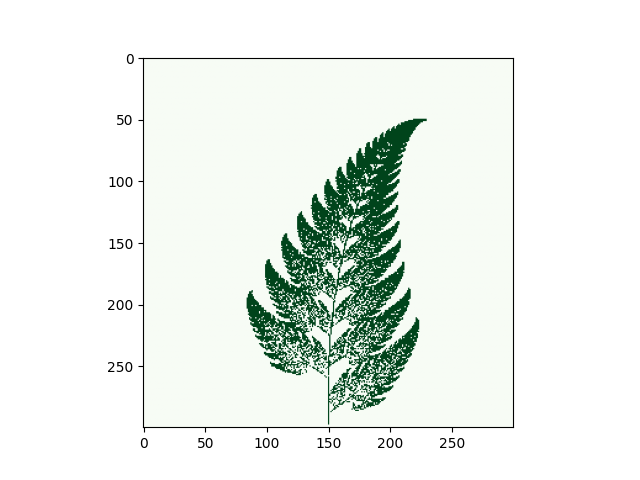
The Barnsley Fern.