Learning Scientific Programming with Python (2nd edition)
E6.12: Finding a best-fit straight line
A straight-line best fit is just a special case of a polynomial least-squares fit (with deg=1). Consider the following data giving the absorbance over a path length of 55 mm of UV light at 280 nm, $A$, by a protein as a function of the concentration, $[\mathrm{P}]$:
| $[P] / \mathrm{\mu g.mL^{-1}}$ | $A$ |
|---|---|
| 0 | 2.287 |
| 20 | 3.528 |
| 40 | 4.336 |
| 80 | 6.909 |
| 120 | 8.274 |
| 180 | 12.855 |
| 260 | 16.085 |
| 400 | 24.797 |
| 800 | 49.058 |
| 1500 | 89.400 |
We expect the absorbance to be linearly related to the protein concentration: $A = m[\mathrm{P}] + A_0$ where $A_0$ is the absorbance in the absence of protein (for example, due to the solvent and experimental components).
import numpy as np
import matplotlib.pyplot as plt
Polynomial = np.polynomial.Polynomial
# The data: conc = [P] and absorbance, A
conc = np.array([0, 20, 40, 80, 120, 180, 260, 400, 800, 1500])
A = np.array(
[2.287, 3.528, 4.336, 6.909, 8.274, 12.855, 16.085, 24.797, 49.058, 89.400]
)
cmin, cmax = min(conc), max(conc)
pfit, stats = Polynomial.fit(
conc, A, 1, full=True, window=(cmin, cmax), domain=(cmin, cmax)
)
print("Raw fit results:", pfit, stats, sep="\n")
A0, m = pfit
resid, rank, sing_val, rcond = stats
rms = np.sqrt(resid[0] / len(A))
print(f"Fit: A = {m:.3f}[P] + {A0:.3f}(rms residual = {rms:.4f})")
plt.plot(conc, A, "o")
plt.plot(conc, pfit(conc))
plt.xlabel(r"[P] /$\mathrm{\mu g\cdot mL^{-1}}$")
plt.ylabel("Absorbance")
plt.show()The output shows a good straight-line fit to the data:
Raw fit results:
poly([ 1.92896129 0.0583057 ])
[array([ 2.47932733]), 2, array([ 1.26633786, 0.62959385]), 2.2204460492503131e-15]
Fit: A = 0.058[P] + 1.929 (rms residual = 0.4979)
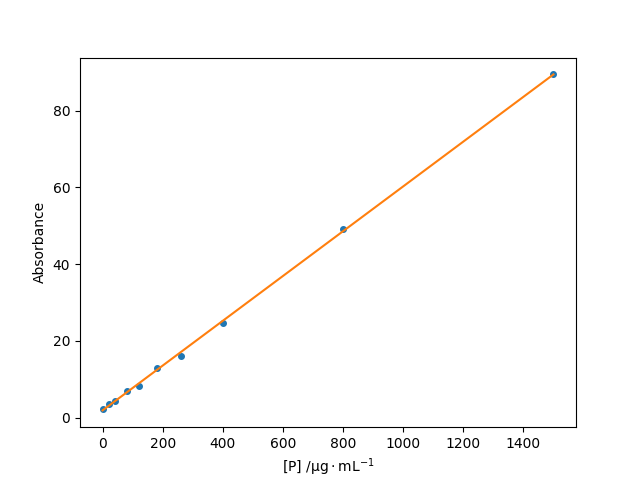
A best fit line to light absorbance as a function of protein concentration.