Learning Scientific Programming with Python (2nd edition)
E6.13: Creating a rotation matrix in NumPy
The two dimensional rotation matrix which rotates points in the $xy$ plane anti-clockwise through an angle $\theta$ about the origin is
$$ \mathbf{R} = \left(\begin{array}{rr}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right). $$
To create a rotation matrix as a NumPy array for $\theta=30^\circ$, it is simplest to initialize it with as follows:
In [x]: theta = np.radians(30)
In [x]: c, s = np.cos(theta), np.sin(theta)
In [x]: R = np.array(((c, -s), (s, c)))
Out[x]: print(R)
[[ 0.8660254 -0.5 ]
[ 0.5 0.8660254]]
As of NumPy version 2.2 there is still a matrix subclass, which offers a Matlab-like syntax for manipulating matrices, but its use is no longer encouraged and (with luck) it will be removed in future.
Derivation 1
Since rotations are linear transformations, the effect of rotating a vector from the origin to some arbitrary point, $P = (x, y)$, can be established by considering the rotation of the basis vectors $\hat{\boldsymbol{e}}_x \equiv (1,0)$ and $\hat{\boldsymbol{e}}_y \equiv (0,1)$. In the figure below, a rotation by $\theta$ takes
$$ \begin{align*} \hat{\boldsymbol{e}}_x &\rightarrow \hat{\boldsymbol{e}}_x' = \cos\theta\hat{\boldsymbol{e}}_x + \sin\theta\hat{\boldsymbol{e}}_y, \\ \hat{\boldsymbol{e}}_y &\rightarrow \hat{\boldsymbol{e}}_y' = -\sin\theta\hat{\boldsymbol{e}}_x + \cos\theta\hat{\boldsymbol{e}}_y. \end{align*} $$
Our point $P$ is therefore transformed from $(x, y) \equiv x\hat{\boldsymbol{e}}_x + y \hat{\boldsymbol{e}}_y$ to: $$ \begin{align*} P' = x\hat{\boldsymbol{e}}_x' + y \hat{\boldsymbol{e}}_y' = (x\cos\theta - y\sin\theta)\hat{\boldsymbol{e}}_x + (x\sin\theta + y\sin\theta)\hat{\boldsymbol{e}}_y. \end{align*} $$ That is, $$ \begin{align*} P' = \mathbf{R}P = \left(\begin{array}{rr}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right)\left(\begin{array}{r}x \\ y \end{array}\right). \end{align*} $$
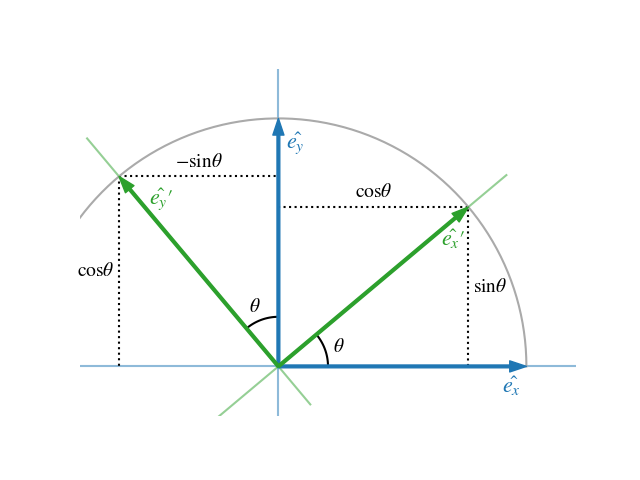
Rotation of a coordinate system in 2D
Derivation 2
Consider the point $P$ in polar coordinates: $P = (x, y) = (r\cos\phi, r\sin\phi)$. Rotation by an angle $\theta$ takes $$ \begin{align*} P \rightarrow P' &= (r\cos(\phi+\theta), r\sin(\phi+\theta)) \\ &= (r[\cos\phi\cos\theta - \sin\phi\sin\theta], r[\cos\phi\sin\theta + \sin\phi\cos\theta])\\ &= (x\cos\theta - y\sin\theta, x\sin\theta + y\cos\theta)\\ &= \left(\begin{array}{rr}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{array}\right)\left(\begin{array}{r}x \\ y \end{array}\right). \end{align*} $$