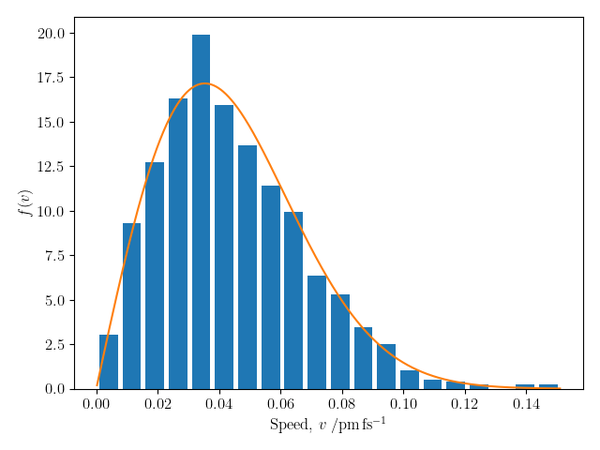
The code below uses the above Vector2D class to implement a simple molecular dynamics simulation of circular particles with identical masses moving in two dimensions. All particles initially have the same speed; the collisions equilibrate the speeds to the Maxwell–Boltzmann distribution, as demonstrated by the figure shown below.
Note: whilst elegant, the object-oriented approach taken here is not the fastest: there is an overhead to instantiating multiple objects, which becomes significant when many particles and collisions need to be considered at each time step. For a faster, NumPy-only approach, see this page, which provides a script to generate an animation of a two-dimensional gas.
import math
import random
import matplotlib.pyplot as plt
from vector2d import Vector2D
class Particle:
"""A circular particle of unit mass with position and velocity."""
def __init__(self, x, y, vx, vy, radius=0.01):
self.pos = Vector2D(x, y)
self.vel = Vector2D(vx, vy)
self.radius = radius
def advance(self, dt):
"""Advance the particle's position according to its velocity."""
# Use periodic boundary conditions: a Particle that moves across an
# edge of the domain 0<=x<1, 0<=y<1 magically reappears at the opposite
# edge.
self.pos = (self.pos + self.vel * dt) % 1
def distance_to(self, other):
"""Return the distance from this Particle to other Particle."""
return self.pos.distance_to(other.pos)
def get_speed(self):
"""Return the speed of the Particle from its velocity."""
return abs(self.vel)
class Simulation:
"""A simple simulation of circular particles in motion."""
def __init__(self, nparticles=100, radius=0.01, v0=0.05):
self.nparticles = nparticles
self.radius = radius
# Randomly initialize the particles' positions and velocity directions.
self.particles = [self.init_particle(v0) for i in range(nparticles)]
self.t = 0
def init_particle(self, v0=0.05):
"""Return a new Particle object with random position and velocity.
The position is chosen uniformly from 0 <= x < 1, 0 <= y < 1;
The velocity has fixed magnitude, v0, but random direction.
"""
x, y = random.random(), random.random()
theta = 2*math.pi * random.random()
self.v0 = v0
vx, vy = self.v0 * math.cos(theta), self.v0 * math.sin(theta)
return Particle(x, y, vx, vy, self.radius)
def advance(self, dt):
"""Advance the Simulation by dt in time, handling collisions."""
self.t += dt
for particle in self.particles:
particle.advance(dt)
# Find all distinct pairs of Particles currently undergoing a collision.
colliding_pair = []
for i in range(self.nparticles):
pi = self.particles[i]
for j in range(i+1, self.nparticles):
pj = self.particles[j]
# pi collides with pj if their separation is less than twice
# their radius.
if pi.distance_to(pj) < 2 * self.radius:
colliding_pair.append((i, j))
print('ncollisions =', len(colliding_pair))
# For each pair, the velocities change according to the kinetics of
# an elastic collision between circles.
for i,j in colliding_pair:
p1, p2 = self.particles[i], self.particles[j]
r1, r2 = p1.pos, p2.pos
v1, v2 = p1.vel, p2.vel
dr, dv = r2 - r1, v2 - v1
dv_dot_dr = dv.dot(dr)
d = r1.distance_to(r2) ** 2
p1.vel = v1 - dv_dot_dr / d * (r1 - r2)
p2.vel = v2 - dv_dot_dr / d * (r2 - r1)
if __name__ == '__main__':
import numpy as np
sim = Simulation(nparticles=1000, radius=0.005, v0=0.05)
dt = 0.02
nit = 500
dnit = nit // 10
for i in range(nit):
if not i % dnit:
print(f'{i}/{nit}')
sim.advance(dt)
# Plot a histogram of the Particles' speeds.
nbins = sim.nparticles // 50
hist, bins, _ = plt.hist([p.get_speed() for p in sim.particles], nbins,
density=True)
v = (bins[1:] + bins[:-1])/2
# The mean kinetic energy per Particle.
KE = sim.v0**2 / 2
# The Maxwell-Boltzmann equilibrium distribution of speeds.
a = 1 / 2 / KE
f = 2*a * v * np.exp(-a*v**2)
plt.plot(v, f)
plt.show()