Learning Scientific Programming with Python (2nd edition)
E8.22: Two-dimensional interpolation with scipy.interpolate.griddata
The code below illustrates the different kinds of interpolation method available for scipy.interpolate.griddata using 400 points chosen randomly from an interesting function.
import numpy as np
from scipy.interpolate import griddata
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 100)
y = np.linspace(-1, 1, 100)
X, Y = np.meshgrid(x, y)
def f(x, y):
s = np.hypot(x, y)
phi = np.arctan2(y, x)
tau = s + s * (1 - s) / 5 * np.sin(6 * phi)
return 5 * (1 - tau) + tau
T = f(X, Y)
# Choose npts random point from the discrete domain of our model function
npts = 400
px, py = np.random.choice(x, npts), np.random.choice(y, npts)
fig, ax = plt.subplots(nrows=2, ncols=2)
# Plot the model function and the randomly selected sample points
ax[0, 0].contourf(X, Y, T)
ax[0, 0].scatter(px, py, c="k", alpha=0.2, marker=".")
ax[0, 0].set_title("Sample points on f(X,Y)")
# Interpolate using three different methods and plot
for i, method in enumerate(("nearest", "linear", "cubic")):
Ti = griddata((px, py), f(px, py), (X, Y), method=method)
r, c = (i + 1) // 2, (i + 1) % 2
ax[r, c].contourf(X, Y, Ti)
ax[r, c].set_title(f"method = '{method}'")
plt.tight_layout()
plt.show()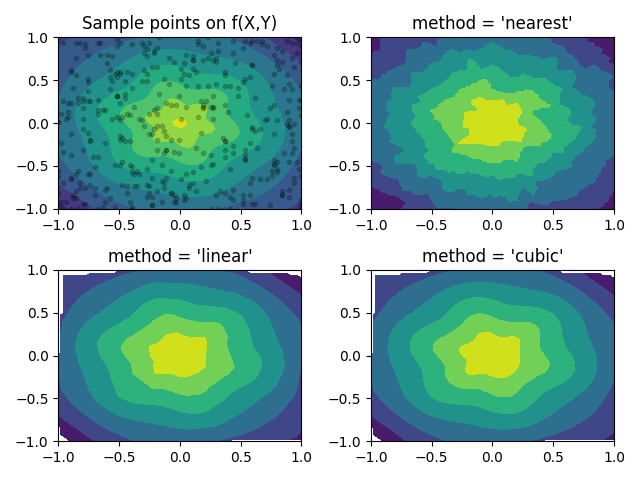
Some different interpolation schemes for `scipy.interpolate.griddata`.